LSAT Forum
3 postsPage 1 of 1
-

- ManhattanPrepLSAT1
-
Thanks Received: 1909
-
Atticus Finch

- Posts: 2851
- Joined: October 07th, 2009
-

- sno7
-
Thanks Received: 1
-
Vinny Gambini

- Posts: 6
- Joined: October 24th, 2013
- This post thanked 1 time.
Re: Q8
hnadgauda Wrote:For this question, I used the strategy of plugging in each answer and if there was ambiguity in the diagram, I moved on to the next answer choice. Is this the best strategy for this type of question?
Thank you!
I find that, for finding out which element's position determines everyone else's, it is usually better to try the answer choice that locks the position of a "stray" or "free radical" element.
Well, maybe there is a more efficient approach for this question type, but at least it proved to be very effective for this question and another question just like this (PT 58, Game 1, Question 3).
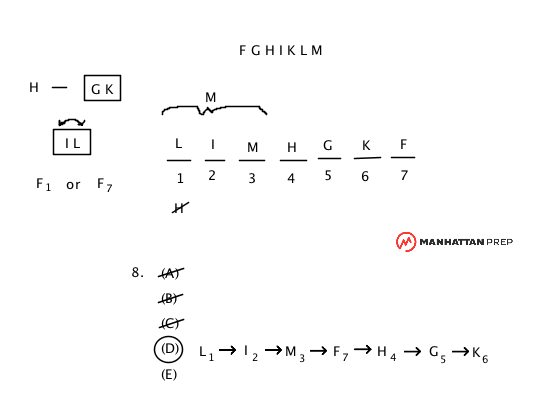
In this game, we don't have a "stray" element. So, what is/are the one(s) with the least amount of constraints?
Well, it's I & L.
Both I and L can go anywhere (at least they seem to be) as long as the other one is next to it on either side.
Then I look for answer choices that deal with these elements.
I see that (C) has I in 2 and (D) has L in 1.
Well, if we put I in 2 (like Answer Choice (C) does), L can still go in either 1 or 3...
BUT if we put L in 1 (like Answer Choice (D) does), I MUST go in 2.
Answer Choice (D) looks more promising than (C) does.
So, I try (D), and it locks the position of I in 2, then F in 7, M in 3, and other three spots for the H-[GK] block.
In this way, I was able to solve this question with trying only one answer choice fully and one other answer choice for a brief moment and not trying any of the other three.
3 posts Page 1 of 1
