LSAT Forum
2 postsPage 1 of 1
-

- timmydoeslsat
-
Thanks Received: 887
-
Atticus Finch

- Posts: 1136
- Joined: June 20th, 2011

- Most Thanked

- First Responder
Re: Q4
I have included the global rules and set up in my explanation, as this is obviously important for completing these local questions.
We know that this is a linear sequencing game. We know that G must be in either 3 or 4. We know that we have a sequencing line of F-L-M-H. We also know that P is a random variable, as it has no rules governing its use.
#4 is a local question that asks us what must be true if M is not 5.
At this point, M's placement is extremely limited. We know M cannot be last (6). We know it cannot be first or second. With this new information given of M not being 5th, it could be in either 3 or 4. We also know that G must be in either 3 or 4. I would run two hypotheticals at this point to show what must be true. Run a hypothetical with M in 3 and then with M in 4.
The rest falls into place nicely. Once M is in 3, we know G is in 4. There is no way that F or L could be in slots 5 or 6. We know that F must precede L, which means F is in 1 and L is in 2. At this point we have slots 5 and 6 open. We have yet to place our random variable P and H. The only rule governing H is that it follows M, and it will do so in slot 5 or slot 6, so this rule is no longer even applicable to us. Thus, P and H can trade off in these spots, as nothing forces these variables to be in certain places.
The second hypothetical of M in 4 will necessitate G in 3. This is the same story as last time, in which F and L could never be in the last two slots. We know F must precede L, so we have F in 1 and L in 2. We also know, like last time, that P and H can trade off in the last two slots.
So our answer of what must be true is that L is in 2 (A).
For #6, this local question asks what must be true if we have an LM block. Well, we can infer some things by combining our global rules with this local information.
We use F - LM - H to now attack the question. I, again, would run two hypotheticals to see what could be true. I would show this tree in a G3 situation and this tree in a G4 situation.
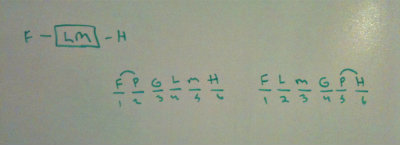
The G3 situation would force the LM block to be placed in slots 4-5. This forces H to be last. This now allows F to trade off with P in slots 1 and 2.
The G4 situation would force the LM block in 2-3. This forces F in slot 1. We now have H and P to trade off in the last two slots. So what could be true? (A) H in slot 5.
We know that this is a linear sequencing game. We know that G must be in either 3 or 4. We know that we have a sequencing line of F-L-M-H. We also know that P is a random variable, as it has no rules governing its use.
#4 is a local question that asks us what must be true if M is not 5.
At this point, M's placement is extremely limited. We know M cannot be last (6). We know it cannot be first or second. With this new information given of M not being 5th, it could be in either 3 or 4. We also know that G must be in either 3 or 4. I would run two hypotheticals at this point to show what must be true. Run a hypothetical with M in 3 and then with M in 4.
The rest falls into place nicely. Once M is in 3, we know G is in 4. There is no way that F or L could be in slots 5 or 6. We know that F must precede L, which means F is in 1 and L is in 2. At this point we have slots 5 and 6 open. We have yet to place our random variable P and H. The only rule governing H is that it follows M, and it will do so in slot 5 or slot 6, so this rule is no longer even applicable to us. Thus, P and H can trade off in these spots, as nothing forces these variables to be in certain places.
The second hypothetical of M in 4 will necessitate G in 3. This is the same story as last time, in which F and L could never be in the last two slots. We know F must precede L, so we have F in 1 and L in 2. We also know, like last time, that P and H can trade off in the last two slots.
So our answer of what must be true is that L is in 2 (A).
For #6, this local question asks what must be true if we have an LM block. Well, we can infer some things by combining our global rules with this local information.
We use F - LM - H to now attack the question. I, again, would run two hypotheticals to see what could be true. I would show this tree in a G3 situation and this tree in a G4 situation.
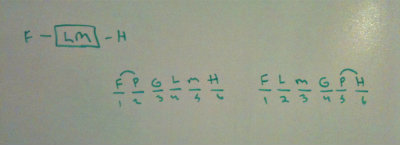
The G3 situation would force the LM block to be placed in slots 4-5. This forces H to be last. This now allows F to trade off with P in slots 1 and 2.
The G4 situation would force the LM block in 2-3. This forces F in slot 1. We now have H and P to trade off in the last two slots. So what could be true? (A) H in slot 5.
2 posts Page 1 of 1
