Q3

[hilarykustoff]

Can someone please explain this one? Thanks!

[timmydoeslsat]

Can someone please explain this one? Thanks!

This is how my global diagram looked:



I used a multi row ordering layout with one row for the boys and one for the girls. I have 7 variables in all with 10 total slots. I am using an X to denote a slot that is not going to be used, so you could say that I will have 3 X's to account for the outstanding 3 slots (7 given variables in a 10 slot layout will give us 3 empty slots that will be filled with X's.)

This type of layout is also beneficial in that I can clearly see that a shared locker must be shared between a boy and a girl.

Question 3 asks us for what is a complete and accurate list of the lockers that cannot be shared given a scenario. This scenario is the boys being consecutively placed in the lockers, with J being 5th.

We know that J shares a locker, and since there are only 3 girls, and R doesn't share a locker, he will share it either with N or T. N/T are interchangeable variables in this game, as are M and P.



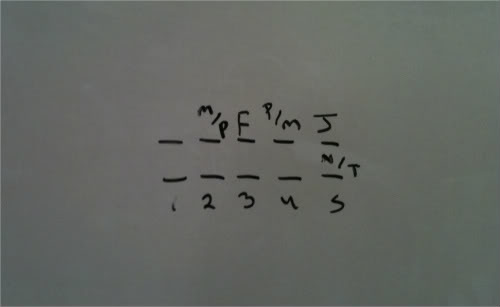
Also, this question stem gave us the inference as to how we will line up the boys consecutively, since they told us that J is 5th. This allows us to infer that the consecutive lining of them goes from 2-5, as anything other than that will have gaps between the boys.

This allows us to infer that R will be first. She cannot share a locker with a boy, and the boys are filling up slots 2-5. We also know that with J being 5th, and also required to have a shared locker, which is 1 of N/T, we know that slot 4 cannot be a shared locker. What girl could go there? It cannot be R and it cannot be the other of N/T, due to the rules stating that those two cannot have adjacent lockers.

Thus, our complete and accurate list is lockers 1,4.

Notice that the other of N/T can be in locker 2 or 3, which is why those lockers are not ones that cannot be shared, as they clearly can be.

[hilarykustoff]

Thanks!!!