Q22 - If the price it pays for coffee

[ohthatpatrick]

Question Type:
Inference (must be true)

Stimulus Breakdown:
Read to combine claims using Conditional, Causal, Quantitative, or Comparison/Contrast wording:
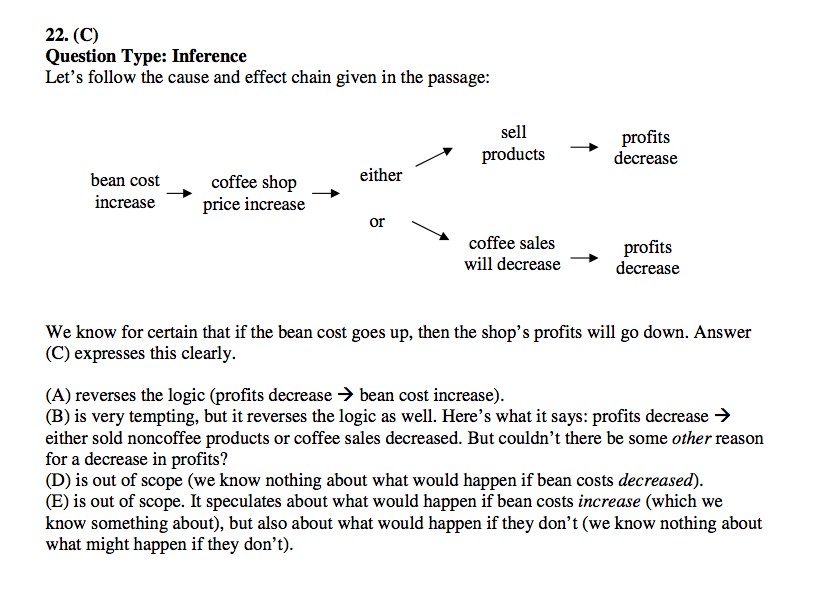
We have a few conditionals, so we should see if they chain together.
If the price of beans goes up -> CS prices go up.
If CS prices go up -> they'll start selling noncoffee or less coffee.
Selling noncoffee stuff would lower profits.
And selling less coffee would decrease profits.

Answer Anticipation:
Putting that together, it sounds like CS is gonna have lower profits if the price of beans goes up. More specifically, if price of beans goes up -> CS increases prices -> starts selling noncoffee stuff (which decreases profits) or sells less coffee (which decreases profits).

Correct Answer:
C

Answer Choice Analysis:
(A) Illegal reversal. We know "if beans' price goes up -> profit goes down", but this reads backwards.

(B) Illegal reversal. We know "if sell noncoffee stuff or coffee sales go down -> profit decreases".

(C) Correct! "price of beans keeps going up -> profit goes down".

(D) This says "price of beans goes down -> profit goes down".
In other words, we could infer X -> Y, and this answer is saying "~X -> Y".

(E) We're not limited to these two options. It's possible that the price of coffee stays where it is and CS's coffee sales also stay where they are.

Takeaway/Pattern: When given multiple conditionals, we want to see if they chain together. If they do, the correct answer is normally rewarding us for connecting the first idea in the chain to the last (often by presenting us with the contrapositive of that connection in the correct answer). Whenever they test conditional logic, we have to be on the lookout for illegal negations and reversals, such as A and B.

#officialexplanation

[dan]