Q20

[nlynes]

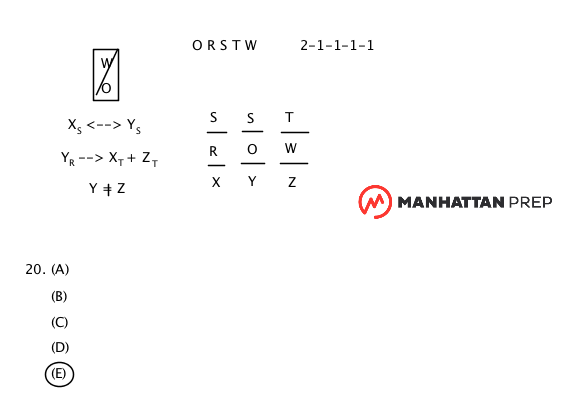
I need help on question 20. I can not figure out what the answer is.

Thank you

[nlynes]

The question that states if Nation z exports tea and wheat then which one of the folowing must be true?

Thanks

[timmydoeslsat]

Understanding this question will entail an understanding of the rules.

We do have a biconditional rule in the setup of this game, introduced by "if but only if."

X(S) <---> Y(S)

The arrow travels in both directions. If X has Soybeans, so does Y. If Y has Soybeans, so does X.

The presence of one of these will guarantee the presence of the other. The absence of one of these will guarantee the absence of the other.

So in the context of #20, we have a local question asking what must be true if Z has both T and W.

We know that each crop must be used at least once. Z's exports is filled up, as each country exports exactly two crops. This means that X and Y must have S. Where else can the S go?

So we know this:

_ _ T
S S W
------
X Y Z

We have not placed O and R. So we must decide where to place them in the remaining two spots.

We have this rule that will kick:

Y(R) ---> X(T) and Z(T)

There is no chance that X will carry T, as we would not be able to place all of our variables at least once. If T went into X, how could we place both O and R in this game?

So this will allow us to infer that Y will not carry R. This means that X must carry R and Y must carry O.

We know that Y must carry soybeans. You really did not even have to do that extra work on this question, but it could prove fruitful for a global question and being able to eliminate answer choices.

[ManhattanPrepLSAT1]

Q20

[ShehryarB30]

Why is B wrong. If T is in Z, that means it can go in in X too if R is in X which is a bicondition so why is E more important?