Q16

[lldknyll26]

Please explain how the answer is B. If Hannah is spending as many days as possible in Nomo and as few days as possible in each of the other cities, how can she visit four cities in country Y. If she's visiting four cities, thats 8 days minimum.

[timmydoeslsat]

Please explain how the answer is B. If Hannah is spending as many days as possible in Nomo and as few days as possible in each of the other cities, how can she visit four cities in country Y. If she's visiting four cities, thats 8 days minimum.

An usual game that is predicated on numerical distribution.

My set up for this game



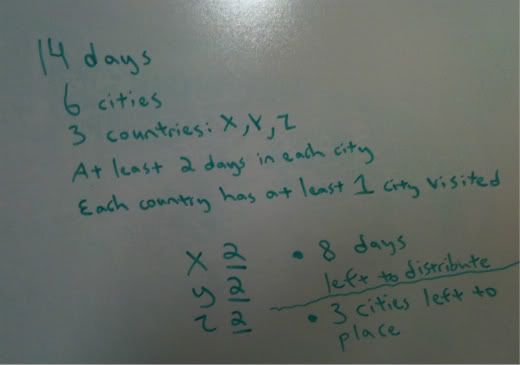
We know that each country is used by having at least one of its cities visited. We know that at least 2 days must be spent in a city.

This means that we can tally up a minimum of 6 days being spent in those 3 countries before we even approach the questions. We will have 3 cities that will move around the game, as well as the number of days spent in respective cities.

Question #14

We are told that Nomo is in country X. We want Hannah to spend as many days as possible in this city of Nomo and as few as possible in EACH of the OTHER cities.

This means that of our 6 cities, 5 of them MUST have 2 days being spent there. If we do not distribute it in that manner, then we are not meeting the demands of this question.

We know that each country has a city visited. We are going to hold off judgement on what to do with country X, as we have a city in question that we want to have a lot of days, so I will not give it 2 days just yet. I know the city must have at least two though.

Countries Y and Z must each have a city that is visited for 2 days.

Notice that what happens to other 3 blocks of 2 day visits does not matter!

All that matters is that 5 of the 6 cities must be visited for 2 days.

That is 5 cities X 2 days = 10 days. We have 14 days that we must use, thus Nomo must have 4 days in its visit.

We can distribute those 3 blocks of 2 day visits to the Y country or the Z country or the X country! Each country could have 4 cities visited.

The test writers simply chose Y. It must be true that Y CAN have four cities.

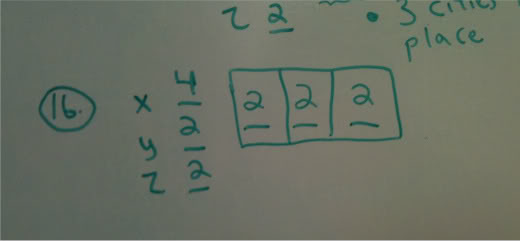
[alex.cheng.2012]

I don't have anything to contribute, but as timmy said, the keyword is CAN.
Call it complaining if you will, but I thought that was pretty tricky on LSAC's part. It's almost like a could be true answer is the correct answer choice for a must be true question.

Y can have 4 cities. Alternatively, couldn't Y and Z swap thereby making Z have 4 cities? Since the question stem only asks for maximum days in city Nomo, and minimum days for the rest of the cities (with no specification to country), couldn't we technically give Y and Z one city each, and then pile the rest into X? Nomo can still have 4 days, and the rest of the cities still being 2 days each.

Perhaps my thinking is flawed, it's been a long day. But the aforementioned is why I think the answer is almost like a could be true answer.