LSAT Forum
5 postsPage 1 of 1
-

- timmydoeslsat
-
Thanks Received: 887
-
Atticus Finch

- Posts: 1136
- Joined: June 20th, 2011
- This post thanked 1 time.

- Most Thanked

- First Responder
Re: Q1
The diagram you have looks great.
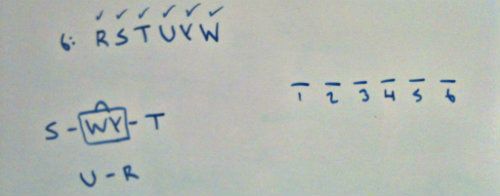
Question 1 is the usual logic game question asking us to find the one answer choice that has a valid hypothetical. We take one rule and apply it to all answer choices until we have one answer choice left.
A) Does not have S before the WY reversible block
B) Does not have T following the WY reversible block
C) Does not have the WY reversible block
D) Does not have U before R
E)
Answer choice (E) wins by default.
Question 2 is a global question asking us how many variables could be first. By looking at our global diagram, we can see that only two options are possible to be first. It is either S or it is U. We have no floaters. The answer is two (B).
Question 3 is a global question asking for a time where U cannot go. Looking at our global diagram, we know that the only obvious answer would be last, but we know the testwriters will not make it that easy. We now have to consider U's placement with regard to the WY reversible block. Obviously there would be no issue with U being 1 or 5.
Where an issue could occur is the realization that only two possible variables can go first. If you place U third, you would force S to be first. But now we have an impossibility. Who will go second? It cannot be R, as R cannot come before U. And it could not be W or Y, as they couldnt form a block in spots 2 and 3 because U is in three. The answer is that U cannot go third (C).
If you could not think this one through, there is nothing wrong with skipping it and saving for the last question. This way you would have previous work from other questions in which you could see all of the places where U went with no problem.
Question 5 is a local question asking what must be true if T is in four. We can see from our global diagram that T has exactly three variables that must precede it, so we know that these variables must take up the available 1-3 slots in this order S - WY reversible block.
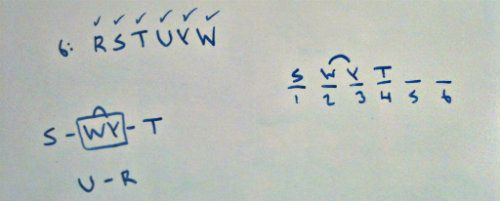
As for slots 5 and 6, we know that we only have two variables left: U and R. We know that there is an order associated with those two: U-R. So we know U is fifth and R is sixth.
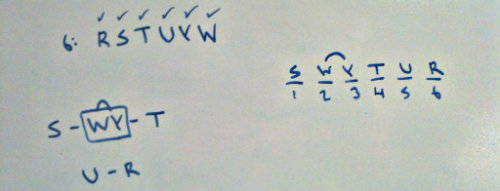
Question 6 is essentially wanting a valid order of the variables without the W. So we now have two ordering trees:
S - Y - T
U - R
(E) is the only one that has both tree orderings kept.
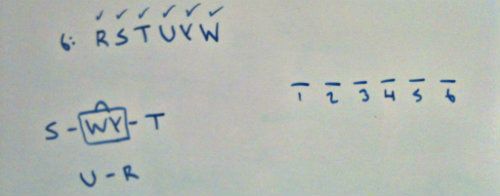
Question 1 is the usual logic game question asking us to find the one answer choice that has a valid hypothetical. We take one rule and apply it to all answer choices until we have one answer choice left.
A) Does not have S before the WY reversible block
B) Does not have T following the WY reversible block
C) Does not have the WY reversible block
D) Does not have U before R
E)
Answer choice (E) wins by default.
Question 2 is a global question asking us how many variables could be first. By looking at our global diagram, we can see that only two options are possible to be first. It is either S or it is U. We have no floaters. The answer is two (B).
Question 3 is a global question asking for a time where U cannot go. Looking at our global diagram, we know that the only obvious answer would be last, but we know the testwriters will not make it that easy. We now have to consider U's placement with regard to the WY reversible block. Obviously there would be no issue with U being 1 or 5.
Where an issue could occur is the realization that only two possible variables can go first. If you place U third, you would force S to be first. But now we have an impossibility. Who will go second? It cannot be R, as R cannot come before U. And it could not be W or Y, as they couldnt form a block in spots 2 and 3 because U is in three. The answer is that U cannot go third (C).
If you could not think this one through, there is nothing wrong with skipping it and saving for the last question. This way you would have previous work from other questions in which you could see all of the places where U went with no problem.
Question 5 is a local question asking what must be true if T is in four. We can see from our global diagram that T has exactly three variables that must precede it, so we know that these variables must take up the available 1-3 slots in this order S - WY reversible block.
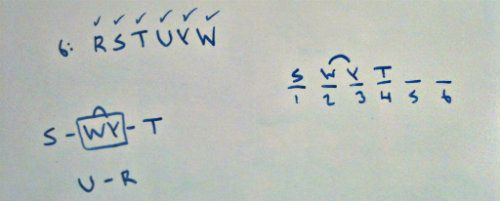
As for slots 5 and 6, we know that we only have two variables left: U and R. We know that there is an order associated with those two: U-R. So we know U is fifth and R is sixth.
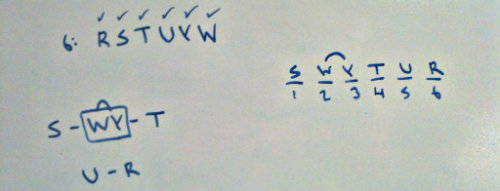
Question 6 is essentially wanting a valid order of the variables without the W. So we now have two ordering trees:
S - Y - T
U - R
(E) is the only one that has both tree orderings kept.
5 posts Page 1 of 1
