Set Up:

This reminds me of the Zephyr Airlines game of course. We can view this game as an assignment game with the board variables being used from within.
The first rule is that N has more than K. With our initial setup information of this game, we can infer that since K must have at least 1 connection, this means that N must have at least 2 connections. We also can remember that the highest number of connections a variable can have is four, as a park cannot connect with itself.

The next rule is a not rule that we must remember to place on both parks.

The next rule tells us that M has more connections than N. We know that N has at least 2, so this means that M must have at least 3. When we initially considered the maximum number of connections a park can have, we realized it is four. With the not rule of J for M, the most M can have is in fact 3, and we know that M must have 3 connections. This means that we can now wall off M and it must have KLN as its connections.
We can also infer that since M must have 3 connections, N must have 2 connections exactly and K having exactly 1 connection.
Since we have placed KLN into M, we must now distribute the M into those places, as this board works from within itself.
This is what we have going into the questions:
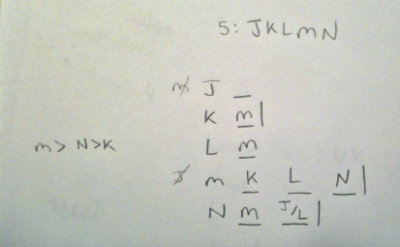
#1:
A global must be true question.
We know (A) must be true.
#2:
The toughest part about this question and others like it is the wording.
"Which one of the following represents a complete and accurate list of parks to which North Park could be directly connected?"
This is the equivalent of asking for what is a complete and accurate list of any park that could be connected to N. We are literally looking for a laundry list of variables that be with N.
We know that there are 3: M, J, and L. Answer choice C.
Answer choice D would be correct if the question asked us what could be a complete and accurate list of parks connected to N. Notice where the could be language is in the question stem.
#3:
A local question asking for what must be true if N is with J. This really only has a consequence for what L can do. L has missed out on a chance to have a connection with N since N is now walled off with M and J. L cannot go with N, K, or itself. This leaves only J that it could be with now since we know L is already with M.
So we know that it must be true that the maximum number of connections L could have is 2. This is answer choice A.
#4:
A global must be false question. I am going to start from A and work my way down.
A) We know N is with 2 and I see no reason why L cannot have 3 right now.
B) I see no reason why J cannot have 2.
C) This one is interesting in that it brings up the two variables that do not have definitive placements already. I will keep this to check if nothing else stands out.
D) See no reason why this cannot work.
E) Same thing.
So I go back to look at C again.
This answer choice will now place every park into a walled-off situation. For L to have 3 parks, it must be the case that every park available must have a connection to it. So now L has MNJ. But now every park is completely full except J, which still has one spot left. This proves that this answer choice must be false.

