Logic Game Challenge #34: Party Problem (Easy)

[wingedfeetxc]

Discuss amongst yourselves.

[timmydoeslsat]

I did this game after completing the hard version.

I do the in-out games differently than what Manhattan LSAT teaches, but it really is the same concept.

I will explain my initial set up.

The rules are:

M ---> S

L ---> ~O and ~P

~M ---> L and R

* Note: This rule is the "at least one" rule. It must be the case that at least one of "M" or "L and R" is present. It could be the case that both are present according to this one rule in isolation, but to have both precluded is unacceptable.

1 of S/T in, 1 of S/T out

The important take-away is that N is a random variable and that O and P are interchangeable variables.

I also see initially that M and T can never be at the party together.

For question #1, I go through my rules, choosing the first rule of M--->S and apply it through answer choices A through E. I am able to eliminate D.

The second rule of L ---> ~O and ~P eliminates A.

The third rule of ~M ---> L and R eliminates none of the answer choices.

The fourth rule of one of S and T being in and the other being out eliminates E and C. For choice C, it is important to realize that having neither one of S and T would mean that both would be out, which is unacceptable according to our rule of one being in.

Our answer is B.

For question #2, this is a global question of what must be true.

I could hold off on this question and wait for more hypotheticals to build up from local questions, but I am feeling that I can determine something that must be true based on my set up. If I do not see anything that catches my interest, I will move on from this question.

The first choice of A does catch my attention because I notice that P can be matched up with S in some form.

If I have P...I do not have L....if I do not have L....I have M....if I have M....I have S.

So there is no way for P to accompany T to the party because if P attends, S attends. We know that the S and T have to be split up among the in and out and column because of rule #4.

Answer choice A must be true.

For question #3, we have a local question asking us what must be false if Matt does not attend the party.

~M ---> L and R must both be in.

L ---> ~O and ~P

We also know that one of S and T will go on each side of the columns and it does not matter where they go because the rule affecting their selection was with the condition of M being selected. In this case M is not selected, so S is now random because it is not controlled by the rules any longer.

We also have a true random variable of N also out there. There must be at least 3 people in and at least 4 people out. The placement of N will cause either 4 to be in or 5 to be out.

It must be false that five people attend the party. Not enough variables available to make this happen.

Answer choice E must be false.

For question #4, we have a local question telling us that if Oscar attends the party what does NOT have to be a must be true situation.

O ---> ~ L

If we do not have L, we must have M. If we have M, we must have S. This means that T has to be out because of our last rule.

P is governed by what happens when L is in. L is out, so it is a random because it is not affected by any rules at this point.

N is a true random.

R is governed by what happens when M is out. With M being in, R is free to do anything.

Answer choice D, R goes to the party, is not something that must be true, thus it is our correct answer.

For question 5, we have a maximum question. On maximum questions, start with the answer choices that are the highest. In this case, we know that 8 is not a viable answer choice because we know that at least one of S and T must be out. We go to the next highest, 7. To make this work, every variable must be in other than one of S/T. This would not work because L being in would cause O and P to go out, giving us three total in the out column.

This makes me want to place L out so that we avoid that situation.

This gives me the ability to have 6 in. I would need to make S go to the party so M can stay in. But this works.

Answer choice C is the answer.

For question #6, we are looking for something that could be true if T went to the party.

T ---> ~S ---> ~M

By M going out, we know that both L and R are going to the party. So we also know that with L being in, that O and P are both out.

This gives us TLR being in and SMOP being out with N free to roam.

Choice C tells us that R attends and that N does not. We know that R attends. N's placement is random, so it could be the case that N does not go. This is not something that must be false. This is the answer.

[brapmocker]

i like the game concept. when will it be release?

[timmydoeslsat]

The games are released every fortnight! This game is part of Manhattan's Logic Game Challenge.

You can find all of their games here:

http://www.manhattanlsat.com/logic-game ... loc=forums


I believe that is what you were asking. If not, please clarify!

[ptraye]

I did this game after completing the hard version.

I do the in-out games differently than what Manhattan LSAT teaches, but it really is the same concept.

I will explain my initial set up.

The rules are:

M ---> S

L ---> ~O and ~P

~M ---> L and R

* Note: This rule is the "at least one" rule. It must be the case that at least one of "M" or "L and R" is present. It could be the case that both are present according to this one rule in isolation, but to have both precluded is unacceptable.

How did you symbolize the 3rd rule like that? The rule says, "Matt will come to the party unless both Lance and Reena do."

[ptraye]

The rules are:

M ---> S

L ---> ~O and ~P

~M ---> L and R

* Note: This rule is the "at least one" rule. It must be the case that at least one of "M" or "L and R" is present. It could be the case that both are present according to this one rule in isolation, but to have both precluded is unacceptable.

Rule #3: Matt will come to the party unless both Lance and Reena do.

When I symbolize this rule I see: If not both Lance and Reena, then Matt will come. -L & -R --> M

Contrapositive: -M --> L or R

[ptraye]

The rules are:

M ---> S

L ---> ~O and ~P

~M ---> L and R

* Note: This rule is the "at least one" rule. It must be the case that at least one of "M" or "L and R" is present. It could be the case that both are present according to this one rule in isolation, but to have both precluded is unacceptable.

Also, would you explain the "at least one" rule to me?

[timmydoeslsat]

The rule in question is: Matt will come to the party unless both Lance and Reena do.

The unless rule when diagramming dictates that what comes after unless is the necessary condition. We will leave that part as given to us. What comes before the unless part is the sufficient condition. We will negate this. Even if it was already negated, we negate it again to make it a positive.

If you have situation where there is nothing before the unless, such as:

Statement 1: Unless B happens, A happens.

We want to realize that what follows after the unless is still the necessary and we still leave it in its current form, and then we begin to search for what is the sufficient condition, which will be tacked on after the necessary is stated. We then negate this sufficient condition.

So to diagram Statement 1: ~A ---> B

Back to our rule: Matt will come to the party unless both Lance and Reena do.

~M ---> L and R

We can see with our mind's eye (I am currently working on getting that trademarked) that the contrapositive is:

~L or ~R ---> M

As for the "at least one" rule, which is what I regard as maybe the most powerful inference you will pick up in your study, we can understand it as follows:

The at least one rule is another way of saying that it is NOT possible for two variables to be out.

The structure you see for this to happen is:

~ [__] ----> [__]

When you see the sufficient condition that is negated and a necessary condition that is positive, you have a situation of at least one variable occurring.

For example:

~A ---> B

Could I ever have both A and B out?

What happens if A is out? B is in.

What happens if B is out? The contrapositive shows us that A is in.

Notice that both variables could be in. What we know MUST be true is that at least one of A and B is in.

The same concept works in the opposite way.

[__] ---> ~[__]

A ---> ~B

At least one is out!

Both could be out, but at least one must be out at all times!

It cannot be true that both A and B are in.

[ivelinavp]

For question #3, we have a local question asking us what must be false if Matt does not attend the party.

~M ---> L and R must both be in.

L ---> ~O and ~P

We also know that one of S and T will go on each side of the columns and it does not matter where they go because the rule affecting their selection was with the condition of M being selected.In this case M is not selected, so S is now random because it is not controlled by the rules any longer.

Could you please elaborate on why is S not controlled by the rules any more? One of the rules in the game was "if M comes, S will come".
Thank you.

[timmydoeslsat]

Could you please elaborate on why is S not controlled by the rules any more? One of the rules in the game was "if M comes, S will come".
Thank you.

The rule affecting S was:

M ---> S

We have a case of ~M.

At this point S is free to do whatever it wishes. What happens if S is in? We have no rule.

What happens if S is out? Then M is out. We already know that M is out. So either side will work for S.

[amkiap]

Could you please elaborate on why is S not controlled by the rules any more? One of the rules in the game was "if M comes, S will come".
Thank you.

The rule affecting S was:

M ---> S

We have a case of ~M.

At this point S is free to do whatever it wishes. What happens if S is in? We have no rule.

What happens if S is out? Then M is out. We already know that M is out. So either side will work for S.

I'm sorry, but I'm also finding this explanation a little confusing. Rule 1 states that if M goes then S goes...so the contrapositive would be If no S, then no M. Are you saying that now the rule depends on S, so therefore it doesn't matter if M is there or not? To me it just made sense that if M is not there, then S wouldn't be there either, which was why I originally picked (A).

I did have another question though, If L then no O & P, are they saying that if L goes then O can't be there alone (or even P be there alone for that matter)? Or do they mean that if L is there, O nor P can be there? I struggled between (E) and (A).

[raniokoye]

Pretty cool game, very stimulating.

[hyewonkim89]

This game has been killing me for the last 30 minutes..

I got all the rules right and drew the logic chain following the rules. But when I actually got to the questions, I couldn't get most of them right.. And I still don't understand why the right answers are right.. (And this is the easy version.. sigh..)

Could someone please explain #2, 3, 4, and 6 in detail???

Thanks in advance!

PS. In Q6, "Nina" should be changed to "Nick."

[csunnerberg13]

it doesn't seem like anyone is checking this thread anymore - but I second the request for explanations, or at least a diagram set up. Incorporating the third rule into the logic chain is really confusing - how should it be done?

[ohthatpatrick]

Here's how the Logic Chain should look:


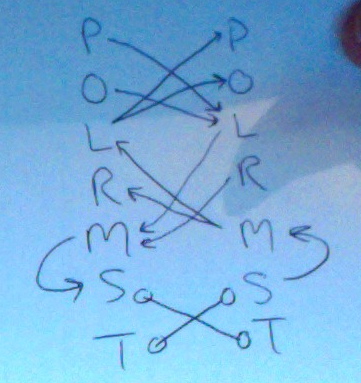
S and T are connected with double-headed arrows (which many of us draw with bubbles on the ends, because a double-headed arrow sometimes gets confusing-looking).

The third rule is
~M --> L and R
which can be split up
~M --> L
and
~M --> R

Its contrapositive is
~L or ~R --> M
which can be split up
~L --> M
and
~R --> M

We can also start this game with some placeholders in the IN/OUT column.

The easiest one is the S/T rule. One must be IN, one OUT. So in your diagram, you should have a S/T placeholder on the IN side and a T/S placeholder on the OUT side.

The third rule gives us a M/LR placeholder on the IN column. M or LR (or all three) will always be in, according to that rule.

The second rule gives us an L/PO placeholder in the OUT column. L or PO (or all three) will always be out, according to that rule.

(For a more detailed explanation, just read timmydoeslsat's awesome posts above).

For those who were struggling with many of the questions, verify that your logic chain is set up correctly. If it was wrong before, try the game again and see if goes better. If it was correct but you still struggled, let us know and we'll elaborate on any of those problems.

[mooknee]

Matt will come to the party unless both Lance and Reena do.

Explanation by Atticus Finch:
The unless rule when diagramming dictates that what comes after unless is the necessary condition. We will leave that part as given to us. What comes before the unless part is the sufficient condition. We will negate this. Even if it was already negated, we negate it again to make it a positive.

I'm confused about this explanation considering the Manhattan Logic Reasoning book (3rd Ed, pg. 347) seems to illustrate the opposite.

Javier arrives to work on time unless (same as except perhaps) there is traffic.

Sufficient. Necessary.
-Traffic --> On Time (Contra) -On Time --> Traffic.

Similarly, Matt will come to the party unless both Lance and Reena do.

-Lance and -Reena --> Matt (C) -Matt --> Lance or Reena.

However, Atticus Finch sees it as ~M ---> L and R.

In one case the 'and' is trigger (way I see it) and in the other it's the outcome (AF) as per same book mentioned above pg. 328.

Just looking for help, please and thank you.

Mike

[GarrettP418]

Javier arrives to work on time unless (same as except perhaps) there is traffic.

Sufficient. Necessary.
-Traffic --> On Time (Contra) -On Time --> Traffic.

Similarly, Matt will come to the party unless both Lance and Reena do.

-Lance and -Reena --> Matt (C) -Matt --> Lance or Reena.

A bit late to be answering now, but there are two rules for translating an "unless" statement into an "if/then" format The first is the more common one (unless --> "if not"), but if there is an "and" in the unless clause, it needs to switch to "or" to make sense. Similarly, if there is an "or" in the unless clause, it switches to "and". There's a brief summary here: https://www.manhattanprep.com/lsat/blog ... 2-minutes/

So in this case, we have "Matt will come to the party unless both Lance and Reena do", so:

M if not L and R translates to:
-L OR -R --> M (C) -M --> L AND R

This makes more sense with the rule: if either L or R skip out on the party, M is coming, but if M is not there, it must mean L and R are both present. Hope this helps anyone with a similar question in the future!