Logic Challenge #27 - Camp Activities

[danny_sklar]

1. D
2. D
3. E
4. E
5. E
6. C

[noah]

1. D
2. D
3. E
4. E
5. E
6. C

Hey there, you should actually submit these straight through the website: http://www.atlaslsat.com/logic-games-practice.cfm as that's where we draw the winner from. But go ahead and post your explanation here....You could win a prize for having the best one.

[audiotechnicaguy]

1) D
2) D
3) B
4) E
5) E
6) C

1) A breaks rule 2, B breaks rule 1, C breaks rule 3, E only has UWBW once

2) If you have S and G on tuesday, you also have them both on wednesday. Tuesday and wednesday are both max 2 spots, UWBW's first spot has nowhere to go at this point, it can't go on wednesday, because that would give wednesday three, which can't happen, it can't go on tuesday (with S on monday), because again, this would give wednesday three events

3) If friday is one event only, monday must be one event, because it can't have all three (because that would break rule 4) and it can't be two because then friday would have all three. So monday is full with just G, Friday is full with just U. we know we need at least one more U, which because S can't be in Monday, must then come on either wednesday or thursday. If it's wednesday, susaphone is on tuesday, and thus on wednesday as well. If U is on Th, then S must be on wed as well.

4) Because the contrapositive of rule 2 is ~F3 --> ~M2, and we know that U cannot go in M, we actually know this rule can be equivalently stated as ~F3 --> M1. Since the max that any day can have is 3, we can write ~F3 as "friday is fewer than 3". Since omonday cannot have U anyway, writing M1 is the same as saying that S cannot go there. Hence F < 3 --> ~Sm

5) This makes U the only thing on tuesday, which makes s on monday, which gives monday exactly 2 (S&G), which gives friday exactly 3. This makes U at least 3 times and SG at most 3 times. Either S or G can be on Thursday, thus allowing S > G as a possibility.

6) this makes friday at most 2, which makes monday 1. wednesday is max 2, but s1 also has to come before u1, thus meaning that T is S only. Th can have all 3. 1 + 1 + 2 + 3 + 2 = 9

[ReadingNation]

So here are the answers I submitted...

1) D
2) D
3) B
4) E
5) E
6) C

So, from now on I refer to each activity by the that activities initial letter ... "S" for sousaphone lessons, "G" for Germanic dance, and "U" for underwater basket-weaving : )

Warning: I wrote the explanation as if I was talking to an LSAT newbie ... : )

Question # 1
1(a), by having only S and U scheduled for Friday while S and G are scheduled for Monday, violates Rule 2, "If exactly two activities are offered on Monday, then exactly three are offered on Friday"

1(b), by only having S and U scheduled for Thursday while S and G are scheduled for Wednesday, violates rule 1, "More activities are offered on Thursday than on Wednesday"

1(c) violates Rule 3, "Any activity offered on Tuesday is also offered on Wednesday" ... While G and U are offered on Tuesday only G is re-offered on Wednesday

1(e) is tricky... though it does not violate any of the indented rules 1(e), by only offering U on Thursday, violates one of the conditions stated in the opening paragraph, "Each activity is offered at least twice"

By process of elimination 1 (D) is correct

Question #2
For a question like #2, it’s always a good idea to scan the answer choices to see which answer choice(s) is more likely to be correct ... So, for question #2, I scanned the answer choices to see which ones would make juicy targets ... Initially, I settled on trying to prove that the situation described in (C) could happen and thereby eliminate (c ) as a potentially correct answer choice ... I came up with the following scenario and in doing so I was able to cross off (C) from the list of potentially correct answer choices M: g and s ... T: u... W: u ... R: g, s, u ... F: g, s, u

Next I settled on (D) ... if "˜g’ and "˜s’ are offered on Tuesday than "˜g’ and "˜s’ also have to be offered on Wednesday ... from here we have two ways we can tackle (D) ... we can decided that the first day "˜s’ is offered in is on Tuesday or we can decide that the first day "˜s’ is offered in is on Monday ... If "˜s’ is first offered on Tuesday than due to the 4th indented rule "˜u’ has to be offered on Wednesday ... but if "˜u’ was offered on Wednesday while "˜g’ and "˜s’ were offered on Tuesday this would lead to a violation of the first rule ... so we can scratch off the first option ... what about the second option, "˜s’ is first offered on Monday... this option essentially leads to the same scenario as the first option ... a violation of Rule 1, albeit through a slightly different route ... If "˜s’ is first offered on Monday than "˜u’ would have to be offered on Tuesday ... but if "˜u’ is offered on Tuesday along with g and s, then all three would have to be offered on Wednesday ... and since there are only 3 activities and all three activities are offered on Wednesday there is no way we would be able to avoid violating rule 1, "More activities are offered on Thursday than on Wednesday" ... so in summary, whereas in the 1st option the 4th rule leads to a direct violation of the 1st rule, in the second option, the 3rd rule leads to a direct violation of the 1st rule

Below is a scenario that satisfies answer choices (a), (b) and (e) without violating any of the rules ... M: g and s ... T: s and u ... W: s and u ... R: g, s and u ... F: g, s and u

[ReadingNation]

Question #3

The first crucial step in solving the third question is realizing how the second rule is activated by the new restriction ... if "˜u’ is the only activity offered on Friday than there cannot be three activities offered on Friday ... taking the second rule into consideration, if Friday does not offer three activities than Monday cannot offer two activities ... this leaves us with two options for Monday, either Monday offers only one activity or it offers all three activities ... however, from the fourth rule you should have been able to deduce that "˜u’ can never be offered on Monday ... hence, the only viable option for Monday is one activity and since the fifth rule states "˜g’ is always offered on Monday that leaves "˜g’ as the only eligible option for Monday
O’k ... so after all that mumbo-gumbo, what do we know? We have Monday and Friday completely figured out, right? O’k, so let’s continue ...

Since "˜s’ was not offered on Monday "˜u’ is not eligible for Tuesday ... since we know that g and s can never go together on Tuesday this allows us to set up a dual diagram:

Option 1: M: g.... T: g ... W: ? ... R: ? ... F: u

Option 2: M: g ... T: s ... W: ? ... R: ? F: u

In the first Option "˜s’ would be forced into Wednesday and Friday, "˜g’ would have to be offered on Wednesday and the first appearance of "˜u’ would have to occur on Thursday ... Given that basic template you could set up two options:

Option 1a): M: g ... T: g ... W: s and g ... R: s and u ... F: u

Option 1b): M: g ... T: g ... W: s and g ... R: s, u and g ... F: u

Take a quick look at the second option ... in it, "˜u’ would have to first be offered on Wednesday and "˜s’ would have to be offered on Wednesday ... given this basic set-up there is only one option that we could set-up for option 2:

Option 2: M: g ... T: s ... W: s and u ... R: s, u and g ... F: u
So why all the work? All three options allow us to easily run through the answer choices and see which one has to be true and which four do not ...

3a) ... the second option proves that Germanic dance does not have to be offered on Tuesday

3c) ... all three options prove that underwater basket-weaving does not have to be offered on Tuesday ... in fact, it's an impossibility

3d) ... if you tackled the question correctly you should have deduced that 3d) along with 3c) was not possible

3e) Options 1a and 1b prove that underwater basket-weaving does not have to be offered on Wednesday

Question #4

The key to question #4 was realizing that the rule in question was a conditional sufficient then necessary relationship ... now, since Rule 2 did not link up with any other conditional rule, we did not have a "˜if a then b then c’ scenario ... what we do have is a "˜if a then b’ scenario ... and what is an equivalent of "˜ if a then b’ ... if not b, the not a, right?

What could be considered "˜not b’ for Rule 2: "3 activities were not offered on Friday" or since there were only three activities in total, "Less than 3 activities were offered on Friday"
What would be the equivalent of "˜not a’ for rule 2: "Two activities were not offered on Monday"

As stated before, in the context of this game, two activities were not offered on Monday would either mean only one activity was offered on Monday or three activities were offered on Monday ... however, s we know that only "˜g’ and "˜s’ are eligible to be offered on Monday because "u" cannot be offered on Monday (thanks to the 4th rule) ... hence, two activities not offered on Monday in conjunction with the 5th rule translates into "˜S cannot be offered on Monday’ ... so let’s take a step back now ... so, what is "˜if not b, then not a’ again ... is it similar to e) : ) ?

Question # 5

The key to the fifth question is to realize how the third rule is being implemented ... if "˜u’ is the only activity offered on Wednesday, and if there is at least one activity offered each day, then according to rule 3 (Any activity offered on Tuesday is also offered on Wednesday) "˜ u’ could be the only activity offered on Tuesday ... once we know that "˜u’ is offered on Tuesday, then according to rule 4, "˜s’ must be offered on Monday ... so now we know "˜s’, along with "˜g’, is offered on Monday, what does that set off? Rule 2, right? So, now we know the following:

M: g and s ... T: u ... W: u ... R: 2 or 3 activities ... F: g, s and u

Given that the fifth question is an "˜each of the following must be false Except" question, the scenario above should be enough to tackle the answer choices

5a) and 5b) ... the deduction we made regarding the conditional statement in the question stem and the third rule should let us know that these answer choices must be false

5c) ... in the set-up above there is only one day that is not completely determined, Thursday ... in order for c) to be true "˜g’ would have to be offered twice on Thursday without "˜u’ being offered ... yet the stipulation in the opening paragraph "no activity is offered more than once in the same day" counteracts this ... hence c), like a) and b) must also be false

5d)... take a look at the set-up above and you’ll realize that, in regard to the stipulation in question 5, what is true of g is true of s ... hence, 5d) must also be false

5e) the following scenario lets us know that 5e) does not have to be false ...

M: g and s ... T: u ... W: u ... R: s and u ... F: g, s and u

[ReadingNation]

Question #6

Remember, no question is set up so you could look cute, stare at it and hope that it tells you it’s secrets ... every question is set-up for a reason, if you don’t stop and try to think why this particular question is being asked you are helping the LSAC ( or in this case Atlas) help you bury your own grave .... So what does the stipulation in Question 6 let us know? If rule two doesn’t come to mind you probably didn’t get this question right. If Thursday is the last day "˜s’ is offered, and there are only three activities, than there cannot be three activities scheduled on Friday ... Once we’re aware of this we are on solid ground ... If Friday does not offer three activities than Monday cannot offer two ... i.e "˜g’ is the only activity offered on Monday
From here, you can set up a dual option, with either "˜s’ or "˜g’ being offered on Tuesday, since in this scenario "˜u’ is not eligible ...

If "˜g’ is offered on Tuesday you could set up the following maxed out scenario ...
M: g ... T: g ... W: g and s ... R: g, s and u ... F: u and g

If "˜s’ is offered on Tuesday you could set up the following maxed out scenario ...
M: g ... T: s ... W: s and u ... R: s, u and g ... F: u and g

In both cases, the maximum number of activities that could be offered is nine

[T.housman31]

I'm slightly confused about question number 4. What disqualifies choice D? I understand why E is correct, but am having trouble understanding how D is incorrect...

Thanks!

[ManhattanPrepLSAT1]

This gets at the heart of conditional logic.

Answer choice (D) reverses the logic of the conditional statement.

Here's an analogy...

If George is late for work, he will be reprimanded.

Does this mean that if George is reprimanded, then George was late for work. Not necessarily. Theoretically, George could have been reprimanded for something else.

The constraint in the game, states that if Monday has two activities, then Friday has three activities. According to this, it could be the case that Friday has three activities, while Monday only has one.

But according to answer choice (D), this possibility would no longer exist, so the constraint is not an even swap.

Does that help clear things up?

[T.housman31]

Thanks for the response! I understand, but doesn't the question ask what would have the same effect? Does D not have the same effect? I know D and E mean different things, but they result in the same distribution don't they?

Thanks for the help!

[rippinradio]

Choice D precludes solutions which are acceptable under the original conditions, such as the following two:

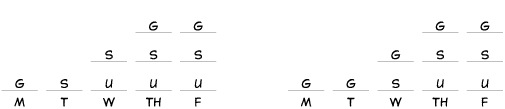
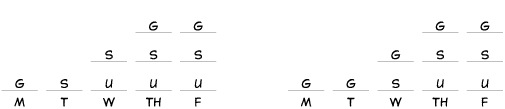
[ManhattanPrepLSAT1]

That's great work rippinradio! I couldn't have said it any better myself.

Does that clear things up T.housman31? If there are situations that would be acceptable under one constraint, but not the other, that implies that the two constraints are not an even substitution.

[giladedelman]

And the winner is ... Reading Nation!

Thanks so much to everyone who submitted responses (and thanks even to those who played along but didn't post)! We hope you enjoy playing our Logic Challenges as much as we enjoy creating them.

[anorawang]

Where can I find answers/explanations to 27. Toss Toss Toss?

[maryadkins]

Toss Toss Toss is 28 not 27 and it is here: https://www.manhattanprep.com/lsat/foru ... t1303.html