1. E
2. B
3. E
4. E
5. B
6. A
Explanations (and challenge, hopefully) to follow.
LSAT Forum
11 postsPage 1 of 1
-

- monica.ann.mark
-
Thanks Received: 0
- Forum Guests
- Posts: 2
- Joined: February 08th, 2010
-

- j.s.cummins
-
Thanks Received: 0
- Forum Guests
- Posts: 1
- Joined: February 08th, 2010
Re: Fortnightly Logic Challenge #21 - The College Comedy Tour
here's my go at it:
1) E
2) B
3) E
4) C
5) B
6) A
7) D
1) E
2) B
3) E
4) C
5) B
6) A
7) D
-

- mattdallavis23
-
Thanks Received: 0
- Forum Guests
- Posts: 1
- Joined: January 28th, 2010
Re: Fortnightly Logic Challenge #21 - The College Comedy Tour
Here you are:
1) E
2) B
3) D
4) C
5) B
6) A
7) D
1) E
2) B
3) D
4) C
5) B
6) A
7) D
-

- Lsat
-
Thanks Received: 0
- Forum Guests
- Posts: 2
- Joined: July 22nd, 2009
Re: Fortnightly Logic Challenge #21 - The College Comedy Tour
The answer is:
1. E
2. B
3. C
4. C
5. B
6. B
7. C
1. E
2. B
3. C
4. C
5. B
6. B
7. C
-

- jonathanleslie73
-
Thanks Received: 0
- Forum Guests
- Posts: 2
- Joined: November 16th, 2009
Re: Fortnightly Logic Challenge #21 - The College Comedy Tour
I believe that a previous poster hit it right on the nose, so in the interests of winning, let me try an explanation. First, a representation of the rules would be helpful:
1. R-> XP, XS
2. Q-> XS, XT
3. W-> T/U, x[TU]
1. Which one of the following could be a complete and accurate list of the schools at which she performs?
(A) Queens, Rice, Wellesley, Vermont
(B) Queens, Rice, Tufts, Vermont, Wellesley
(C) Rice, Tufts, Utah, Wellesley
(D) Rice, Stanford, Tufts, Wellesley
(E) Penn, Stanford, Tufts, Vermont, Wellesley
We plug through the first two rules and rule out (C), (B) immediately. Then, look at the third rule and are obliged to rule out (A) and (D), as they violate both parts of it, respectively. Thus, we are left with (E.) Of course, if we chance upon testing (E) before (A) or (D) with the third rule, then we would already know we have the answer.
2. If she performs at Wellesley and Vermont, but not Utah, then she could also perform at any one of the following schools EXCEPT:
(A) Penn
(B) Queens
(C) Rice
(D) Stanford
(E) Tufts
The first step is to think of what these mean. If W is the case, and not U (V is something of a "wild card"), then "T" is also the case. This, in turn, means that Q cannot be true, qua rule two; therefore (B) is the answer.
3. If she performs at exactly four schools, including Tufts and Utah, the schools at which she does NOT perform could include any of the following pairs EXCEPT:
(A) Wellesley and Stanford
(B) Queens and Stanford
(C) Vermont and Rice
(D) Penn and Rice
(E) Stanford and Vermont
Small diagram (top row is schools she does and bottom, school's she doesn't), making appropriate inferences:
T U _ _
W Q _ _
(According to rule three, W could NOT be true, if both T and U are; likewise, in accord with rule two, Q is NOT true, if T is.)
We can start with the prospective answers that don't include the colleges we already know she will not perform at, viz. W, Q. If we're smart, we'll start with the one that includes V, as this is the only college that doesn't have a rule governing it and therefor by excluding it, you're more like to limit your options. So we can even scribble in S and V lightly, so we can erase it if were wrong (this is what I would do.) Anyway, we see that the only two colleges left, as it were, for her to perform at, would be Penn and Rice, which is a quite literally impossible achievement according to rule one. So we're done. Of course, if we go through the other two we would see that they are possible.
4. If she performs at exactly five schools, and does NOT perform at Rice, it could be true that she performs at neither
(A) Vermont nor Stanford
(B) Vermont nor Tufts
(C) Tufts nor Queens
(D) Tufts nor Utah
(E) Queens nor Stanford
Another small diagram, likewise configured:
_ _ _ _ _
R _ _
The first step is to deal with what directly affects those two empty spaces, which is whether or not Q is included in them. Quite simply, if it is not, the only answer is that R, S, and T are the schools she skips, in accordance with rule two. As S and T are not an option, we know the answer must include Q, so we scribble that in:
R Q _
The other rule with which to wrestle is then the third, which says that not all W T U can be visited, so we look at the choices and we see that (C) includes both Q and T. Viola.
5. If she performs at Rice, what is the maximum number of schools that could be included in the tour?
(A) 6
(B) 5
(C) 4
(D) 3
(E) 2
Another diagram, or rather, dual list:
R
P S
We know that either Q or T, but not both, will be visited. But if T is visited, then, we know, qua rule three, that this will limit the total amount of colleges visited, more than if Q were visited. So Q is visited, and then two out of the three W, U, T, are visited. Leaving us with 5 total visits, which is (B.)
6. If she performs at exactly five schools, including Stanford and Vermont, the schools at which she does NOT perform could include any of the following EXCEPT:
(A) Penn
(B) Queens
(C) Rice
(D) Tufts
(E) Utah
ANother diagram, making basic inferences:
S V _ _ _
R _ _
One could do this by process of elimination, granting that the answer obviously cannot be (C), but the best way to think about would be to start with the proposed un-visited school that would mean nothing for the other schools in this context. Because R is not visited, if P is not visited, then this is redundant in a certain way, according to the logic of this game. So it's worth trying first, off hand:
S V _ _ _
R P _
Indeed, then, we see that, if Q is not visited, then we violate rule three, and, vice versa, then we are forced to violate rule two.
Challenge Problem _ Not for the faint of heart...
7. If she performs at exactly five schools, how many different groupings of schools (disregarding the order visited) are possible?
(A) 8
(B) 7
(C) 6
(D) 5
(E) 4
If we are smart, then we will think back question 5, where we inferred that there was precisely one combination there:
R Q W U V
P S T
The next question is what Q does; we immediately recognize that there is only therefore one combination when it is included, sans R, with the following excluded: R (duh), S, T.
Then, with both Q and R excluded, the main question is how to deal with rule three:
_ _ _ _ _
Q R _
The answer is that, as precisely one of W U T have to be not visited by her, therefore there are three corresponding conceivable answers (with all the other possibilities neccessarily pre-set).
Three plus one plus one is five. Therfore, the answer is (D.)
1. R-> XP, XS
2. Q-> XS, XT
3. W-> T/U, x[TU]
1. Which one of the following could be a complete and accurate list of the schools at which she performs?
(A) Queens, Rice, Wellesley, Vermont
(B) Queens, Rice, Tufts, Vermont, Wellesley
(C) Rice, Tufts, Utah, Wellesley
(D) Rice, Stanford, Tufts, Wellesley
(E) Penn, Stanford, Tufts, Vermont, Wellesley
We plug through the first two rules and rule out (C), (B) immediately. Then, look at the third rule and are obliged to rule out (A) and (D), as they violate both parts of it, respectively. Thus, we are left with (E.) Of course, if we chance upon testing (E) before (A) or (D) with the third rule, then we would already know we have the answer.
2. If she performs at Wellesley and Vermont, but not Utah, then she could also perform at any one of the following schools EXCEPT:
(A) Penn
(B) Queens
(C) Rice
(D) Stanford
(E) Tufts
The first step is to think of what these mean. If W is the case, and not U (V is something of a "wild card"), then "T" is also the case. This, in turn, means that Q cannot be true, qua rule two; therefore (B) is the answer.
3. If she performs at exactly four schools, including Tufts and Utah, the schools at which she does NOT perform could include any of the following pairs EXCEPT:
(A) Wellesley and Stanford
(B) Queens and Stanford
(C) Vermont and Rice
(D) Penn and Rice
(E) Stanford and Vermont
Small diagram (top row is schools she does and bottom, school's she doesn't), making appropriate inferences:
T U _ _
W Q _ _
(According to rule three, W could NOT be true, if both T and U are; likewise, in accord with rule two, Q is NOT true, if T is.)
We can start with the prospective answers that don't include the colleges we already know she will not perform at, viz. W, Q. If we're smart, we'll start with the one that includes V, as this is the only college that doesn't have a rule governing it and therefor by excluding it, you're more like to limit your options. So we can even scribble in S and V lightly, so we can erase it if were wrong (this is what I would do.) Anyway, we see that the only two colleges left, as it were, for her to perform at, would be Penn and Rice, which is a quite literally impossible achievement according to rule one. So we're done. Of course, if we go through the other two we would see that they are possible.
4. If she performs at exactly five schools, and does NOT perform at Rice, it could be true that she performs at neither
(A) Vermont nor Stanford
(B) Vermont nor Tufts
(C) Tufts nor Queens
(D) Tufts nor Utah
(E) Queens nor Stanford
Another small diagram, likewise configured:
_ _ _ _ _
R _ _
The first step is to deal with what directly affects those two empty spaces, which is whether or not Q is included in them. Quite simply, if it is not, the only answer is that R, S, and T are the schools she skips, in accordance with rule two. As S and T are not an option, we know the answer must include Q, so we scribble that in:
R Q _
The other rule with which to wrestle is then the third, which says that not all W T U can be visited, so we look at the choices and we see that (C) includes both Q and T. Viola.
5. If she performs at Rice, what is the maximum number of schools that could be included in the tour?
(A) 6
(B) 5
(C) 4
(D) 3
(E) 2
Another diagram, or rather, dual list:
R
P S
We know that either Q or T, but not both, will be visited. But if T is visited, then, we know, qua rule three, that this will limit the total amount of colleges visited, more than if Q were visited. So Q is visited, and then two out of the three W, U, T, are visited. Leaving us with 5 total visits, which is (B.)
6. If she performs at exactly five schools, including Stanford and Vermont, the schools at which she does NOT perform could include any of the following EXCEPT:
(A) Penn
(B) Queens
(C) Rice
(D) Tufts
(E) Utah
ANother diagram, making basic inferences:
S V _ _ _
R _ _
One could do this by process of elimination, granting that the answer obviously cannot be (C), but the best way to think about would be to start with the proposed un-visited school that would mean nothing for the other schools in this context. Because R is not visited, if P is not visited, then this is redundant in a certain way, according to the logic of this game. So it's worth trying first, off hand:
S V _ _ _
R P _
Indeed, then, we see that, if Q is not visited, then we violate rule three, and, vice versa, then we are forced to violate rule two.
Challenge Problem _ Not for the faint of heart...
7. If she performs at exactly five schools, how many different groupings of schools (disregarding the order visited) are possible?
(A) 8
(B) 7
(C) 6
(D) 5
(E) 4
If we are smart, then we will think back question 5, where we inferred that there was precisely one combination there:
R Q W U V
P S T
The next question is what Q does; we immediately recognize that there is only therefore one combination when it is included, sans R, with the following excluded: R (duh), S, T.
Then, with both Q and R excluded, the main question is how to deal with rule three:
_ _ _ _ _
Q R _
The answer is that, as precisely one of W U T have to be not visited by her, therefore there are three corresponding conceivable answers (with all the other possibilities neccessarily pre-set).
Three plus one plus one is five. Therfore, the answer is (D.)
-

- tad.kim
-
Thanks Received: 0
- Forum Guests
- Posts: 3
- Joined: December 08th, 2009
Re: Fortnightly Logic Challenge #21 - The College Comedy Tour
My answer...
1. E
2. B
3. C,E both possible
4. C
5. B
6. A
7. D
1. E
2. B
3. C,E both possible
4. C
5. B
6. A
7. D
-

- jiehaep
-
Thanks Received: 15
- LSAT Geek
- Posts: 17
- Joined: June 30th, 2009
Re: Fortnightly Logic Challenge #21 - The College Comedy Tour
Hey gang,
Kudos to jonathanleslie for some very elegant solutions! When games such as this appear, with almost nothing to diagram beyond the given constraints (unlike other games in which helpful second level inferences are easily diagrammable before attacking the questions), one of the hardest things for many test-takers to do is "grab onto" something in what otherwise seems to be a crank-it-out approach. jonathanleslie was methodical and ruthless--well done.
One very minor quibble-- the answer given is correct, but the constraints referenced in the explanation for number 1 don't align to the eliminated choices as I read them--are these typos? There's also the possibility I'm missing something... one of the best things about these forums is learning from the different approaches people bring-- I'd be interested to see how you align those choices to those constraints.
Two specific things I dug about jonathanleslie's approach that I'd like to call out: (1) identifying and working around un-constrained elements (V, here), which can be a key to many questions on these types of games; and (2) referring back to work from previous questions, which is a HUGE help here, since several of the questions reference the same scenario (5 schools in, 3 schools out). There's one more question I can see for which some time might be shaved off by referencing a past question, especially if your brain isn't naturally as methodical as jonathanleslie's...any guesses on which question, which it could refer back to, and how?
Kudos to jonathanleslie for some very elegant solutions! When games such as this appear, with almost nothing to diagram beyond the given constraints (unlike other games in which helpful second level inferences are easily diagrammable before attacking the questions), one of the hardest things for many test-takers to do is "grab onto" something in what otherwise seems to be a crank-it-out approach. jonathanleslie was methodical and ruthless--well done.
One very minor quibble-- the answer given is correct, but the constraints referenced in the explanation for number 1 don't align to the eliminated choices as I read them--are these typos? There's also the possibility I'm missing something... one of the best things about these forums is learning from the different approaches people bring-- I'd be interested to see how you align those choices to those constraints.
Two specific things I dug about jonathanleslie's approach that I'd like to call out: (1) identifying and working around un-constrained elements (V, here), which can be a key to many questions on these types of games; and (2) referring back to work from previous questions, which is a HUGE help here, since several of the questions reference the same scenario (5 schools in, 3 schools out). There's one more question I can see for which some time might be shaved off by referencing a past question, especially if your brain isn't naturally as methodical as jonathanleslie's...any guesses on which question, which it could refer back to, and how?
-

- laura.alexander25
-
Thanks Received: 0
- Forum Guests
- Posts: 1
- Joined: November 29th, 2011
Re: Logic Challenge #21 - The College Comedy Tour
On number 3, are C & E both possible? If not, can someone explain why E is the correct answer & why C is not?
Thanks!
Thanks!
-

- timmydoeslsat
-
Thanks Received: 887
-
Atticus Finch

- Posts: 1136
- Joined: June 20th, 2011

- Most Thanked

- First Responder
Re: Logic Challenge #21 - The College Comedy Tour
So we know that T and U are in. This allows us to infer that W is out. For W to be in, we must have one of T/U in, one of T/U out. Since this will not occur, W is out.
We also know that with T in, Q must be out. As for Q to be in, it must be true that both S and T are out.
So we know from the local information given in this question stem that exactly four are in, which means exactly four are out.

So it is now the case that the S conditional rule is void. It also true that the W conditional rule is void. The only rule left to consider is R ---> ~P and ~S. We also know that the other outstanding variable is V, the random variable.
I would show 2 hypotheticals. Show what happens when R is in and then when R is out.
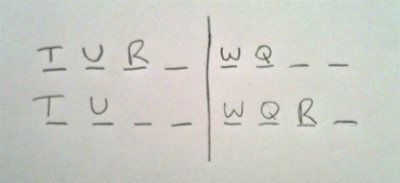
In the first hypothetical, with R being in, this forces P and S out. Our out column is now full. This means the random variable, V, must be in.
In the second hypothetical. Our R conditional rule is now void. This leaves P, S, and V as floaters to do whatever they please.
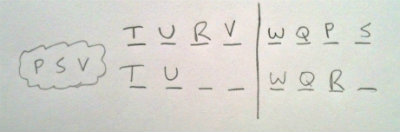
As we can see, it could never be true that S and V are both out.
We also know that with T in, Q must be out. As for Q to be in, it must be true that both S and T are out.
So we know from the local information given in this question stem that exactly four are in, which means exactly four are out.

So it is now the case that the S conditional rule is void. It also true that the W conditional rule is void. The only rule left to consider is R ---> ~P and ~S. We also know that the other outstanding variable is V, the random variable.
I would show 2 hypotheticals. Show what happens when R is in and then when R is out.
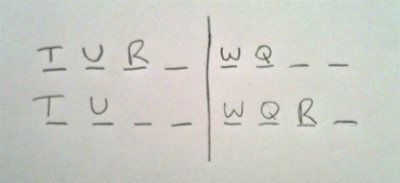
In the first hypothetical, with R being in, this forces P and S out. Our out column is now full. This means the random variable, V, must be in.
In the second hypothetical. Our R conditional rule is now void. This leaves P, S, and V as floaters to do whatever they please.

As we can see, it could never be true that S and V are both out.
-

- jose50_gurr
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 1
- Joined: August 12th, 2015
Re: Logic Challenge #21 - The College Comedy Tour
I don't understand why (D) is the answer to question 7.
7. If she performs at exactly five schools, how many different groupings of schools (disregarding the order visited) are possible?
(A) 8
(B) 7
(C) 6
(D) 5
(E) 4
Are there supposed to be 5 different groups with exactly five schools each?
I am only able to come up with these 4 combinations;
R,V,Q,W,U
Q,V,U,W,P
W,T,V,P,S
W,U,V,P,S
7. If she performs at exactly five schools, how many different groupings of schools (disregarding the order visited) are possible?
(A) 8
(B) 7
(C) 6
(D) 5
(E) 4
Are there supposed to be 5 different groups with exactly five schools each?
I am only able to come up with these 4 combinations;
R,V,Q,W,U
Q,V,U,W,P
W,T,V,P,S
W,U,V,P,S
-

- lanham_charles
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 2
- Joined: December 14th, 2015
Re: Logic Challenge #21 - The College Comedy Tour
(W U)|(Q) | p |(V)
t | s |(R) |
(W T)| s | p |(V)
u|(Q) |(R) |
(W U)| (Q) |(R) |(V)
t |s&t |s&p|
(W U)| s | p |(V)
t |(Q) |(R) |
(T U)| s | p | (V)
w|(Q)| (R)|
t | s |(R) |
(W T)| s | p |(V)
u|(Q) |(R) |
(W U)| (Q) |(R) |(V)
t |s&t |s&p|
(W U)| s | p |(V)
t |(Q) |(R) |
(T U)| s | p | (V)
w|(Q)| (R)|
11 posts Page 1 of 1