This is a standard ordering sequencing game that tests block placement and dual options at a certain spot.
All elements are used in the rules, but it can be noted that if T is not 3rd, it will then act as a floater. No interchangeable variables either.
Below is my global setup.
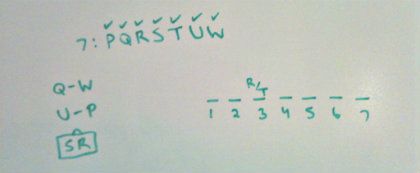
#1 Global question asking us for one single valid hypothetical.
This is where we take a rule and apply it to every answer choice, rinse and repeat.
A) U has to be before P
B) Slot 3 cannot have W.
C) S and R must form a block
D) Q has to be before W.
E) Breaks no rules.
#2 Local question asking us what must be true if W(2) and P(5)
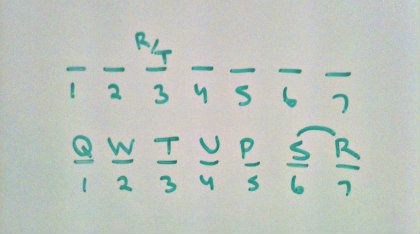
We know that Q must be in 1 for the Q-W to be satisfied. We know that with P being in 5th, U must be in either 3 or 4. Since R or T can be the only variables in slot 3, this forces U into 4. This will now force slot 3 to be T, since R must be side by side with S. We can now fill the last two slots with an option of SR/RS. So we know that (E) must be true.
#3 Local question asking us what must be true if we have a TURS block sequence. I made the additional inference that S is tacked on with R and that P follows the big block due to U being in the block.
The most prudent thing to do at this point is to run 2 hypotheticals. Frame is around who goes 3rd. Show what happens when R is there and when T is there.
Below is what you infer:
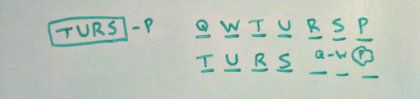
I do make use of Noah's cloud which indicates that P can go into any of the three remaining slots in the second hypothetical. This is because U is already placed second and the only rule that governs P is that it is to follow U, which it will necessarily do in any of those three slots.
#4 Local question asking us what must be false if we have a PS block, which we can make the added inference that it is a PSR block. Even more so, we know that U comes prior to this PSR block.
This allows us to infer that the third slot will not be R due to too many variables coming before R. This means T is third. We can now use the PSR block placement to determine what must be true. Run two hypotheticals of the block sliding from 4-6 and then 5-7.
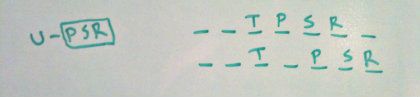
To fill the first hypothetical, we know that the U cannot be last and neither could U. This forces W to be last. We can now have a dual option of Q and U at 1-2.
To fill the second hypothetical, we can just make use of the Q-W order and U as a floater because wherever we place U, it will be ahead of P, which is all that our rules need satisfied.

So what must be false? (B)
T could never be immediately before Q.
#5 Local question asking us what must be true if we have a PTW block. I can make the inference that we must have U and Q precede this box due to the variables W and P being in this box, and we have rules governing the order of those variables.

This is really just the same concept being tested again about who can go third. We now know that T cannot go third as it has too many variables that must precede it, which means R must be third. With R being third, I decide that this may be as easy as knowing that R will precede the 3 variable block of PTW, so I immediately look for an answer discussing R. Bingo, answer choice (D), R must be before P. This answer choice could have used T or W as well in place of P.

