LSAT Forum
6 postsPage 1 of 1
-

- ecmoloney
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 11
- Joined: August 05th, 2009
pt 31-1-G1 - Lockers
Another slow one for me - looking for a better diagram. Any takers?
-

- ManhattanPrepLSAT1
-
Thanks Received: 1909
-
Atticus Finch

- Posts: 2851
- Joined: October 07th, 2009
Re: pt 31-1-G1 - Lockers
So, this game is not terribly challenging, but I think the reason why it was so slow is that there are only a few things you can do before moving into the questions. Most of the work as you move through this game is done with the conditional information contained within the question stem. Notice that 4/6 questions give you conditional information before asking you what must/could/cannot be true.
Attached is a setup for this game and the first two questions explained. If you need more or a specific question explained let me know.
Attached is a setup for this game and the first two questions explained. If you need more or a specific question explained let me know.
-

- namitathakker
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 2
- Joined: November 28th, 2010
Q4
Not sure why the answer to question# 4 is (c) three instead of (b) two.
Here's my setup:
R _ _ _ _
_ _ F _ _
J can't be in locker # 2 because he has to share with one of the girls, who cannot be next to R. So, he must go in locker # 4 or 5. The same logic applies if R is in locker # 5 (J cannot be in #4, directly adjacent to R, so he can only go in #1 or 2).
_ R _ _ _
_ _ F _ _
If R is in locker # 2 or 4, then J cannot be in locker # 1 or 5, respectively, so he can only be assigned to # 4 or 5, or # 1 or 2, respectively.
Any help is greatly appreciated!
Here's my setup:
R _ _ _ _
_ _ F _ _
J can't be in locker # 2 because he has to share with one of the girls, who cannot be next to R. So, he must go in locker # 4 or 5. The same logic applies if R is in locker # 5 (J cannot be in #4, directly adjacent to R, so he can only go in #1 or 2).
_ R _ _ _
_ _ F _ _
If R is in locker # 2 or 4, then J cannot be in locker # 1 or 5, respectively, so he can only be assigned to # 4 or 5, or # 1 or 2, respectively.
Any help is greatly appreciated!
-

- timmydoeslsat
-
Thanks Received: 887
-
Atticus Finch

- Posts: 1136
- Joined: June 20th, 2011

- Most Thanked

- First Responder
Re: Q4
namitathakker Wrote:Not sure why the answer to question# 4 is (c) three instead of (b) two.
Here's my setup:
R _ _ _ _
_ _ F _ _
J can't be in locker # 2 because he has to share with one of the girls, who cannot be next to R. So, he must go in locker # 4 or 5. The same logic applies if R is in locker # 5 (J cannot be in #4, directly adjacent to R, so he can only go in #1 or 2).
_ R _ _ _
_ _ F _ _
If R is in locker # 2 or 4, then J cannot be in locker # 1 or 5, respectively, so he can only be assigned to # 4 or 5, or # 1 or 2, respectively.
Any help is greatly appreciated!
I believe you have misunderstood the rules.
R can be beside another girl. She simply cannot share a locker.
So we know that when we place R somewhere, no other person can go there. And since F is already placed in 3, J can go in three different lockers. We have no rules governing M and P other than the basic idea of them not being able to share a lock with another boy. Thus, we know that one of those guys can comfortably share a locker while J takes the other of N and T, or Fred could too if necessary.
-

- eunjung.shin
-
Thanks Received: 2
-
Jackie Chiles

- Posts: 40
- Joined: December 08th, 2011
Re: pt 31-1-G1 - Lockers
mshermn Wrote:So, this game is not terribly challenging, but I think the reason why it was so slow is that there are only a few things you can do before moving into the questions. Most of the work as you move through this game is done with the conditional information contained within the question stem. Notice that 4/6 questions give you conditional information before asking you what must/could/cannot be true.
Attached is a setup for this game and the first two questions explained. If you need more or a specific question explained let me know.
I dont see the attachment. Can you upload again please?
Much thanks!
-

- timmydoeslsat
-
Thanks Received: 887
-
Atticus Finch

- Posts: 1136
- Joined: June 20th, 2011
- This post thanked 1 time.

- Most Thanked

- First Responder
Re: Diagram
I am going to post my global diagram and step by step explanation for each question.
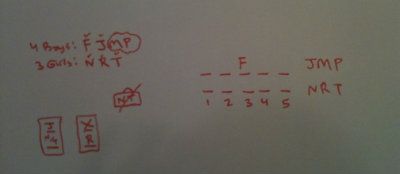
An adequate setup will show each locker having the ability to accommodate two people. We know that if a locker is shared, it must be between a boy and girl. We are not given any special distinction regarding say a bottom part of the locker and a top part of the locker, so it does not matter in this game which variable you place on the top row or bottom row. We can make the setup more visually appealing by reserving one row for the 4 boys and one row for the 3 girls.
We are told that J, a boy, must always share a locker. We are told that R, a girl, must never share a locker.
We are told that F is given locker 3. We also know that girls N and T cannot be beside one another.
When we think about what these rules mean, we can deduce that obviously J must share a locker with either N or T. We know that the two girls, N and T, must share a locker due to the fact that R cannot share one. We will call that slot that is empty above R "X."
We now have 4 slots to place 4 boys so the rest of the girls will necessarily have to share. There is no way for them not to share.
M and P are boys that are not discussed directly in the rules so they are interchangeable in this game. N and T are two interchangeable variables among each other. The same rules are applied to them in the same way.
Question 1
Is a complete and accurate list that must share lockers.
We know J must. Every single answer choice has that. We know that N and T must from our discussion up top. That gives us E. No other choice gives us N and T.
If you did not catch that inference in the setup, you could still get to the right answer rather quickly. Notice that M and P are interchangeable. So if M really was something that must share, then so would P...these variables are interchangeable. Notice that B and D include only one of them. No way that is a complete and accurate list. You are down to (A) (C) and (E). I personally would find the girls more restricting, thus a better candidate to test. Is there any way I could make one of those girls not share a locker. It is a quick test. There is no way.
Question 2
Local question asking what must be true if T is in 3 and M is in 1 by himself.
So we cannot have a girl in locker 1. T, a girl, is in 3. Where can N go is the most prudent question to ask ourselves. N cannot be beside T, so it must go to locker 5. Since R is another girl we have not placed, yet cannot share a locker, this means that J must share with N at locker 5 due to J having to share with someone. We now have two empty lockers at 2 and 4. This will be filled by either R by herself or P by himself. They can switch off at those two respective spots. So our answer is that J must be at locker 5.

Question 3
This is a "what is a complete and accurate list" question asking about those that cannot be a shared locker if it is true that the four boys occupy lockers consecutively with J being in locker 5. Since J is in 5, we must have lockers 5, 4, 3, and 2 be taken up by boys, as this is what we must do to comply with the local condition. This means that locker 1 is empty. This must be where R goes. We know that J is in locker 5, this means that 5 is a shared locker. This means that either N or T is there. This means that locker 4 cannot hold the other of the N/T pair, as they would be next to one another. This means that 4 cannot have a girl present.
The other of N/T can be placed at 2 or 3. So we know that the complete and accurate list is simply lockers 1 and 4. Those can never be shared lockers.
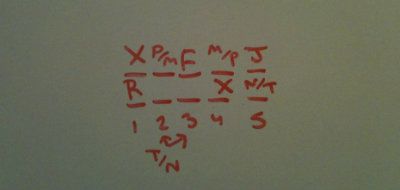
Question 4
This is a global question asking for the maximum number of lockers J can go to once R is placed. We know that the answer cannot be 5, as F is in one of the lockers already. We know that the answer cannot be 4 because R must have a locker all to herself. This means that the maximum number of places J can go is 3.
Question 5
A local question asking what must be true if the first three lockers are assigned to girls. Well we know that locker 2 must go to R so that we can split up the N/T pair. Those 2, N and T, will trade off at slots 1 and 3. With F being in 3 already, this means that J must occupy locker 1 so that he is able to share a locker with someone. This means that lockers 4 and 5 will be two isolated boys, M and P. They are interchangeable and each can go to lockers 4/5.
So we know that J must be assigned to locker 1.
Question 6
A local question asking who must be assigned to locker 4 if lockers 1 and 2 are given to boys that are not sharing them. We know that those two boys must be M and P. So we have three possible slots to place the three girls, slots 3, 4, and 5. We know that the N and T must be separated by R.
So we know that R must go into locker 4.

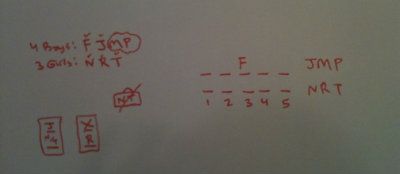
An adequate setup will show each locker having the ability to accommodate two people. We know that if a locker is shared, it must be between a boy and girl. We are not given any special distinction regarding say a bottom part of the locker and a top part of the locker, so it does not matter in this game which variable you place on the top row or bottom row. We can make the setup more visually appealing by reserving one row for the 4 boys and one row for the 3 girls.
We are told that J, a boy, must always share a locker. We are told that R, a girl, must never share a locker.
We are told that F is given locker 3. We also know that girls N and T cannot be beside one another.
When we think about what these rules mean, we can deduce that obviously J must share a locker with either N or T. We know that the two girls, N and T, must share a locker due to the fact that R cannot share one. We will call that slot that is empty above R "X."
We now have 4 slots to place 4 boys so the rest of the girls will necessarily have to share. There is no way for them not to share.
M and P are boys that are not discussed directly in the rules so they are interchangeable in this game. N and T are two interchangeable variables among each other. The same rules are applied to them in the same way.
Question 1
Is a complete and accurate list that must share lockers.
We know J must. Every single answer choice has that. We know that N and T must from our discussion up top. That gives us E. No other choice gives us N and T.
If you did not catch that inference in the setup, you could still get to the right answer rather quickly. Notice that M and P are interchangeable. So if M really was something that must share, then so would P...these variables are interchangeable. Notice that B and D include only one of them. No way that is a complete and accurate list. You are down to (A) (C) and (E). I personally would find the girls more restricting, thus a better candidate to test. Is there any way I could make one of those girls not share a locker. It is a quick test. There is no way.
Question 2
Local question asking what must be true if T is in 3 and M is in 1 by himself.
So we cannot have a girl in locker 1. T, a girl, is in 3. Where can N go is the most prudent question to ask ourselves. N cannot be beside T, so it must go to locker 5. Since R is another girl we have not placed, yet cannot share a locker, this means that J must share with N at locker 5 due to J having to share with someone. We now have two empty lockers at 2 and 4. This will be filled by either R by herself or P by himself. They can switch off at those two respective spots. So our answer is that J must be at locker 5.

Question 3
This is a "what is a complete and accurate list" question asking about those that cannot be a shared locker if it is true that the four boys occupy lockers consecutively with J being in locker 5. Since J is in 5, we must have lockers 5, 4, 3, and 2 be taken up by boys, as this is what we must do to comply with the local condition. This means that locker 1 is empty. This must be where R goes. We know that J is in locker 5, this means that 5 is a shared locker. This means that either N or T is there. This means that locker 4 cannot hold the other of the N/T pair, as they would be next to one another. This means that 4 cannot have a girl present.
The other of N/T can be placed at 2 or 3. So we know that the complete and accurate list is simply lockers 1 and 4. Those can never be shared lockers.
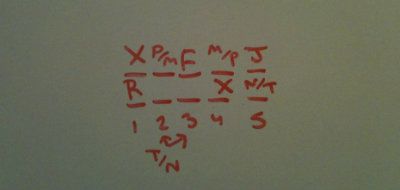
Question 4
This is a global question asking for the maximum number of lockers J can go to once R is placed. We know that the answer cannot be 5, as F is in one of the lockers already. We know that the answer cannot be 4 because R must have a locker all to herself. This means that the maximum number of places J can go is 3.
Question 5
A local question asking what must be true if the first three lockers are assigned to girls. Well we know that locker 2 must go to R so that we can split up the N/T pair. Those 2, N and T, will trade off at slots 1 and 3. With F being in 3 already, this means that J must occupy locker 1 so that he is able to share a locker with someone. This means that lockers 4 and 5 will be two isolated boys, M and P. They are interchangeable and each can go to lockers 4/5.
So we know that J must be assigned to locker 1.
Question 6
A local question asking who must be assigned to locker 4 if lockers 1 and 2 are given to boys that are not sharing them. We know that those two boys must be M and P. So we have three possible slots to place the three girls, slots 3, 4, and 5. We know that the N and T must be separated by R.
So we know that R must go into locker 4.

6 posts Page 1 of 1