these open assignments just kill me....I was doing fine until #15 @ 6min, then somehow i lost it & ended up spending 13 min to finish...does anyone have a diagram I can compare to mine? mine turned out very crazy, that's probably why I had such a hard time...
thanks for all your help! its kind of crunch time so i appreciate any advice!
LSAT Forum
5 postsPage 1 of 1
-

- carmenmarrs
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 6
- Joined: April 20th, 2009
-

- noah
-
Thanks Received: 1192
-
Atticus Finch

- Posts: 1541
- Joined: February 11th, 2009
- This post thanked 1 time.
Re: pt 47, sect 4, game 3
Here's my diagram.
Tell me if you have trouble seeing how to arrive at this. Or perhaps you find an error in my diagram!
For question 16, you end up having to assign R to V and the other Rs are already assigned. That leaves Z with only O or F, and we know that S will carry both of those, since R is not an option since all three of them have been assigned.
Try the game again and tell me how it goes. And in this last few days, I usually suggest that it's time to reinforce what you've learned and work on your strengths, not worry about the parts that are tougher for you. Good luck!
- Noah
Tell me if you have trouble seeing how to arrive at this. Or perhaps you find an error in my diagram!
For question 16, you end up having to assign R to V and the other Rs are already assigned. That leaves Z with only O or F, and we know that S will carry both of those, since R is not an option since all three of them have been assigned.
Try the game again and tell me how it goes. And in this last few days, I usually suggest that it's time to reinforce what you've learned and work on your strengths, not worry about the parts that are tougher for you. Good luck!
- Noah
-

- jamiejames
-
Thanks Received: 3
-
Atticus Finch

- Posts: 116
- Joined: September 17th, 2011
Re: Diagram
I have a question. Because X has more records than any other place, I put a dash on one line for everyone else ( S,T,V, and Z.) Now, because J can only be pin S and X, does that mean I add another line to V and Z?
-

- noah
-
Thanks Received: 1192
-
Atticus Finch

- Posts: 1541
- Joined: February 11th, 2009
Re: Diagram
Yup. That's why there's only two open slots for V and Z.
I'm a bit unclear about your question. If you think there should be only one open slot (the bottom one) for those two, then you're wrong. If that's what you're thinking, what's the third slash for?
I'm a bit unclear about your question. If you think there should be only one open slot (the bottom one) for those two, then you're wrong. If that's what you're thinking, what's the third slash for?
-

- timmydoeslsat
-
Thanks Received: 887
-
Atticus Finch

- Posts: 1136
- Joined: June 20th, 2011

- Most Thanked

- First Responder
Re: Diagram
jeastman Wrote:I have a question. Because X has more records than any other place, I put a dash on one line for everyone else ( S,T,V, and Z.) Now, because J can only be pin S and X, does that mean I add another line to V and Z?
As Noah said, that is right. That is one less slot that V and Z can have.
This is how my diagram looked, although I chose to have lines or slots that indicate that some variable must be placed there rather than the box.
I chose to have the base of my setup be the stores, as I know that each store must have at least 1 of the 4 music types. As of now, I do not even know that every music type will be used.
So I will be assigning FJOR into STVXZ.
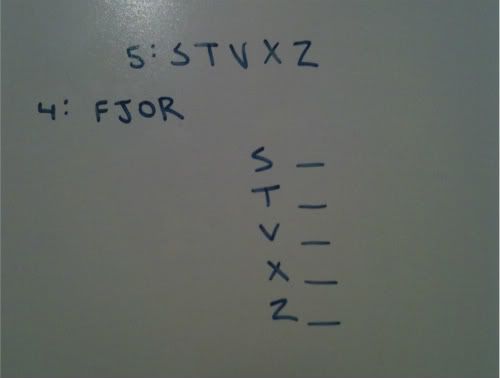
My first rule tells me that I will have exactly 2 J's placed. I indicate this on my diagram to keep track of it.
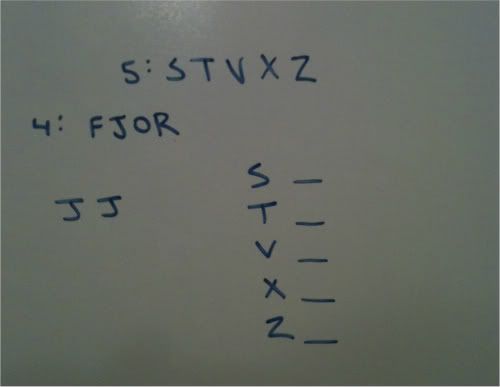
I am then told that T has R and O, and that those are the only ones it carries. I can now wall off this store, as it cannot contain any more music types.
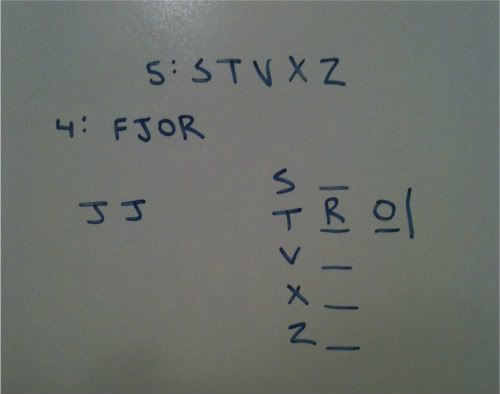
S carries more than T. We know that T carries exactly 2. This means that S must carry at least 3. I will indicate such with 3 lines. It could carry all 4 at this moment, but it is not something that must be true. This is why I will not place the fourth line there. But I will not also wall it off after the 3rd slot.
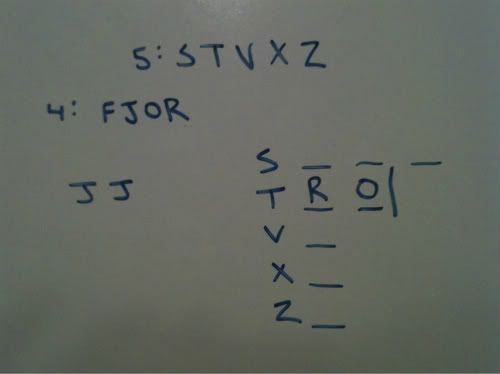
My next rule is that X carries more types of music than any other store. Since I know that S carries at least 3, I know that X must carry all 4 in order for it to have more than any other store.
This also means that S is walled off at 3. It cannot have 4 because at that point X would be tied with a store, and this rule says more than any other store.
With X having four lines, that means it has all four types FJOR. This means that one of our 2 J's is used. I now erase one of the J's. I have one J left to place. As of now, the J must go into either S, V, or Z.
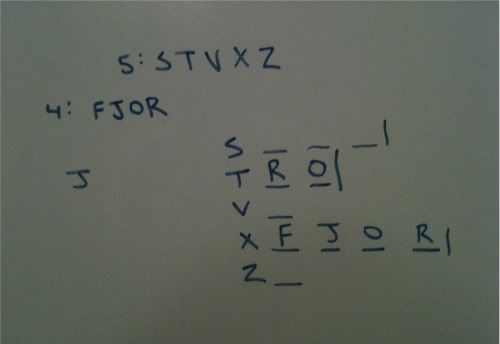
My next rule tells me that S carries J. So now I have no J's left to distribute. I can write ~J beside V and Z. I now only have 2 types left to place in S. It must be 2 of F, O, and R.
My next rule states that V and Z have none in common. So I know that with only 3 variables left in play: FOR....that the maximum amount either V or Z could have is 2. For one of those stores to contain three items is possible. As this would necessarily cause sharing between V and Z.
With this global set up, I see that the issue is going to be the V-Z distinction. S simply has to choose 2 of FOR, and its basis of selection has no impact on the V-Z distinction.
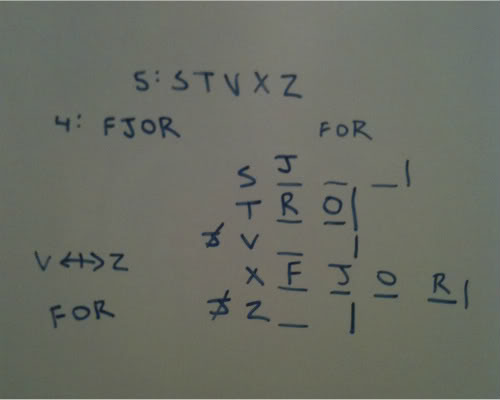
5 posts Page 1 of 1