Diagram

[natalie_lupo]

#17 drove me slightly crazy...

[noah]

December 2004 LSAT Preptest 45 Answers.

Yes, the diagram for this can be a bit daunting. Take a look at how you can keep it neat. Tell me if you have any questions. Good luck!

[andrea.feuer]

I am having trouble drawing my arrows for this statement: "Wendy appears in every photograph that Selma appears in." I thought this means that IF w THEN s because Selma is the necessary part, but from the answer I know its supposed to be the other way around If s Then w, but I don't understand why. Thank you for your help.

[noah]

I am having trouble drawing my arrows for this statement: "Wendy appears in every photograph that Selma appears in." I thought this means that IF w THEN s because Selma is the necessary part, but from the answer I know its supposed to be the other way around If s Then w, but I don't understand why.

Good question - it's crucial to master this sort of thing.

Think about that statement in another context: Wendy shows up to every party that Selma shows up to.

So, which of the following is sufficient to require something (i.e. is a "trigger"):

Selma is there -->

~ Selma is there -->

Wendy shows up -->

~ Wendy shows up -->

Go ahead and figure that out before reading on.


You should have figured out that the first and last ones trigger something. If S is there, then W will come, and if W did not come, then S must not have either - because if S did, W would be there!

The crucial question here is, can Wendy show up in a photograph that Selma is not in? And the answer is yes. W is necessary but not sufficient. S is sufficient but not necessary.

Does that clear it up?

[sranksonly]

Is there an alternate way to diagram this game.Also,Q17 is driving me crazy.I hope this kind of game doesn't appear in October.

[timmydoeslsat]

Is there an alternate way to diagram this game.Also,Q17 is driving me crazy.I hope this kind of game doesn't appear in October.

There is an alternate way of diagramming this game. You can think of this game as a binary grouping game, meaning there are two groups.

You are either in the photograph or you are not in the photograph.



After the first two rules, my diagram looked like that. I also make it a habit to checkmark each variable that is mentioned in the rules. That way I can keep tabs on which variables are randoms/floaters/free agents.

The first two rules are crucial to master.

W appears in every S.

S ---> W

A lot of people are tempted to write this as:

W ---> S

But notice what could happen with this rule.

SSSSSSS
WW

Every time there is a W there is a S. However, we know that this is not what the first rule is telling us. It is telling us that EVERY S is a W. Thus, S ---> W

SSSSSSS
WWWWWWWWWWW

So you could have W's without S's.

I combine the first two rules to create a chain of logic.

The image below shows me also diagramming the next to last rule in our game.



Notice what that ~Y ---> R rule indicates to us.

This tells us that it MUST be the case that at least one of Y and R is IN a photograph.

Consider this analogous situation.

~A ---> B

Contrapositive of that conditional statement?

~B ---> A

Notice that no matter what, at least one of the variables must be in.

What happens if A? We do not know. What happens if B? We do not know. Thus, we could have both A and B.

We know that both cannot be out at the same time because that situation would triggers one of the conditionals.

Time to diagram the last rule, which you can tag along to the first chain of logic.



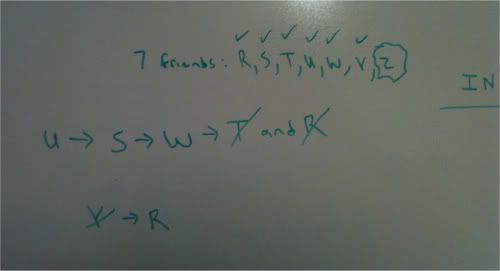
Also notice that I could tag additionally show that when I have R out, that triggers the contrapositive of the second conditional and would give me Y must be in.

Every variable has been checkmarked other than Z, as it has no rules governing it. That means that we can place Z in or out with no issue. That is an important aspect to keep in mind on possible minimum/maximum questions.

Also, we need to know how to properly utilize this approach.

Notice what happens if I have a case of T or R being in.

That sets off the contrapositive, which would give me ~W, ~S, and ~U in that first chain of logic.


QUESTION #13

The first question of this game, #13, is essentially a hypothetical line up question in which a solid grasp of the rules can readily give us an answer.

A) When W is in, R is out. R cannot be in, yet it is.

B) No need to check this one, we got there by process of elimination. You could use this for a future hypothetical in the game. Also notice that you could easily place Z out of this example, as no rules force Z's presence in the photograph.

C) When W is in, R is out. R cannot be in, yet it is.

D) When U is in, S is in, and W is in. Where is W?

E) When U is in, S is in, and W is in. Where is W?


QUESTION #14

This gives us a local rule telling us that if T and Z appear in a photograph together, what must be true?

Well, we know that Z is random, thus, we cannot infer anything from that variable being in. However, we do know that if T is in, that invokes our contrapositive of the first chain. We know that we do not have W, S, or U in the photograph.



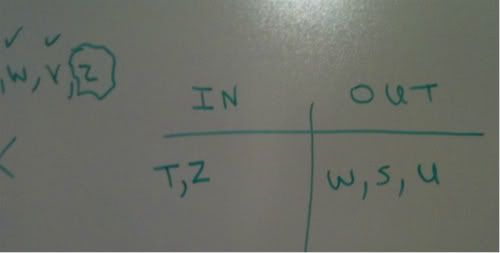
That has placed five of the seven variables. There are two left. Y and R.

We have a rule governing Y and R. At least one must be in! If you cannot recall how we determined that, go back to the beginning of this post to understand this concept.

We can show the consequences of this situation like this:



I have a slot designated for one of R and Y must appearing there. However, I have shown what Noah would call the "cloud of uncertainty!" showing that the opposite of what is selected could go in either place, in or out.

A) Must be false.
B) Could be true, not must be.
C) Must be false.
D) Could be true, not must be.
E) Must be true.


QUESTION #15

If Y does not appear in the photograph, what is the maximum number of friends that could be in the photograph.

Well, we know that if Y is out, that triggers the second conditional, which gives us R being in.

R being in triggers the contrapositive of our first conditional chain of logic, which would give us W, S, and U out.



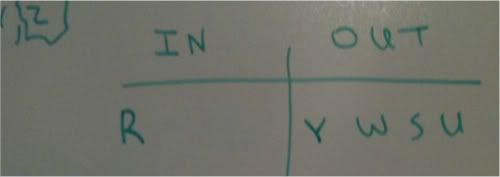
We have placed 5 of the 7 variables. The two that are left to place are T and Z. We have no rules governing what happens with Z.

We also notice that we do not have any rules governing what happens to T at this point.

If T is in, we already have triggered the contrapositive of ~W, ~S, and ~U.

If T is not in, we have no rules governing that.

So both T and Z are random at this point. Since this is asking us for the maximum number of friends that could be in, we must put both of these randoms in the IN PHOTOGRAPH group, as that would give us our true maximum.

Thus, we would have 3.





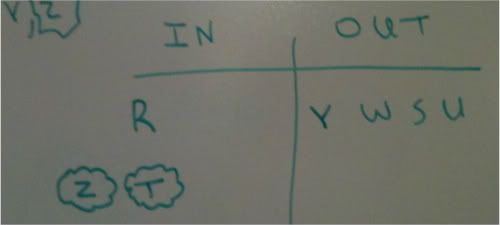
QUESTION #16

This question gives us a local rule of U and Z appearing in a photograph together, and it asks us how many of the OTHER friends MUST appear in the photograph together.

So we have two potential pitfalls in this question if we are not careful. First, we need to point out how many of the OTHER friends are in the photograph, we do not include U and Z in our calculation.

Second, we must consider who MUST be in the photograph. Not could be.

With that said, let's see what we can do. We do not have any rules governing Z, so that gives us nothing. However, we are given U being in. This triggers the first conditional chain of logic.

We know that we will have S, W, and not T and not R.



We also know that if R is out, Y must be in. This is the contrapositive of our second conditional.



We know that three of the other friends MUST be included in the photograph.


QUESTION #17

This is giving us a local rule of there being three friends in this picture. We know then that there must be 4 friends out then.

We need to remember that at least one of those 3 in slots must be given to Y and R.

One of Y and R must always be in.



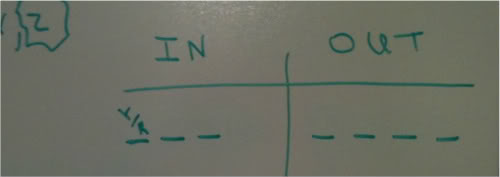
Now we can think about the complications of this rule being combined with the local rule given of only three people being in this photograph.

We realize that U could not be in. If U were in, so would S and W. This would give us too many people in the photograph because at least one of Y and R must always be in.

Look at answer choice A.

Could S and Z be in? No.

If S is in, so is W. That gives us two in. This answer choice also gives us Z. That is three. Where is the space for one of Y and R? There is none.

Thus, this must be false.

[fyami001]

Hi, for number 17, in your explanation for it, I don't understand why Y/R have to be in one of the three in-slots? Please help!

[ohthatpatrick]

Y or R or both always have to be in based on the logic of the 3rd rule.

We would symbolize the 3rd rule as:

~Y --> R
~R --> Y

Can R and Y both be out? No. Because if Y is out, then R must be in. If R is out, then Y must be in.

So it's a guarantee that either R or Y (or both) will always be in.

There are four different ways to write these two letters:

IN | OUT
R | Y
Y | R
RY |
. . .| RY

The first three are possible. The last one is not (according to the rule). So this is a visual way of seeing that we'll always have R, Y, or both in the IN column.

Some of us call these types of rules "placeholders".

Here's how you spot a placeholder:

1. Diagram the conditional and the contrapositive

2. Ask yourself, "Do the two right side ideas refer to the same column?"

3. If so, put a placeholder in that column. If not, there's no placeholder. Move on with your life.

Here's another example:

P --> ~G
G --> ~P

Do both right side ideas refer to the same column? Yes, the OUT column. So we can put a G/P placeholder into the out column.

IN | OUT
. . .| G/P

The conversational way of thinking of this rule is "P and G cannot both be IN." Therefore, at least one of them will always be OUT.

By contrast, here is a NON-placeholder rule.

H --> F
~F --> ~H

Do the two right sides refer to the same column? No. One of them refers to the IN column and the other refers to the OUT column. Therefore, there is no placeholder.

Visually:

IN | OUT
HF |
. . | HF
F | H
H | F

The first three of those are possible. The last one is prohibited by the rule.

There's no placeholder for this type of rule because both could be IN, both could be OUT, or we could have a split.

If you are used to using the Logic Chain for Binary Grouping games, then placeholder rules are the ones in which the arrows cut across the inside. When the arrows go on the outside, there is no placeholder.

COMPLEX PLACEHOLDERS:
Sometimes you get a rule like this ---

F --> ~P and ~R
P or R --> ~F

This is still a placeholder since both right sides refer to the OUT column.

This time, the placeholder would look like:
IN | OUT
. . .| PR/F

In order to satisfy that placeholder, you either need BOTH P and R, or just F by itself.

When you get ugly looking placeholders such as this one, you sometimes decide "ugh. not worth it."

That's totally fine. These can be ugly things to write and look at, and it's possible to get by without them. However, they can also be powerful friends in the world of Binary grouping.

Let me know if you have any questions.

[monicaiannacone]

I understand the diagram and have the same thing, but I'm not understanding why B is correct. Actually, when I do this problem, I keep proving all answer choices as incorrect. Please help, I'm clearly missing something here.

[timmydoeslsat]

I understand the diagram and have the same thing, but I'm not understanding why B is correct. Actually, when I do this problem, I keep proving all answer choices as incorrect. Please help, I'm clearly missing something here.

Are you discussing #13? If so, tell me how you proved B is incorrect.

[monicaiannacone]

After trying this game again, untimed, I realized that I was misunderstanding how to read the logic chain. Now I'm able to diagram the game (6minutes) and answer all questions correctly (8 more minutes) but overall, it took 14 minutes. How can I get faster at this game?

This is what I did:
-Wrote each constraint and contrapositive.
-Made my logic chain diagram with all constraints and contrapositives

Then answered the questions using the logic chain

[ManhattanPrepLSAT1]

Hey Monica,

As we discussed in office hours, skip the step of writing out constraint and then it's contrapositive. You're essentially doubling your work in writing out the constraints twice; first in the individual conditional statements and then once again in the logic chain.

And then repeat, repeat, repeat... That's how you get fast at almost anything!

[matthew.mainen]

This is how I set it up:



http://farm3.staticflickr.com/2809/1072 ... 640b_k.jpg

[stacksdoe]

Hey Monica,

As we discussed in office hours, skip the step of writing out constraint and then it's contrapositive. You're essentially doubling your work in writing out the constraints twice; first in the individual conditional statements and then once again in the logic chain.

And then repeat, repeat, repeat... That's how you get fast at almost anything!

This is also For sranksonly and Matthew:

I essential diagramed the master sketch as Matthew. As for getting faster, as its been stated by the Manhatten rep. its practice, practice is the number one way to gain speed. You also must review your games and look for ways you mayor could have done the game more efficiently. They're a lot of other detail things you could to do to gain speed, but many a time you'll notice things detail things as you practice over and over. I speak from experience. For example, when you read the rules and questions, do you refer to the full name of the variables or do you simple use the first letter? Although its a subtle change, consider that you working with 5-6 questions, reading R instead of Raimundo is more efficient.
Here is my master sketch,similar to Mathew's:
......................... T
U--> S-->W---> +
....................... ~R-->Y
W<--/-->T ( this means W and T cannot both be in)
W<--/-->R (this means W and R can both be in)
~R<--/-->~Y ( this means R and Y can not both be out)
Z= Floater

Monica, they're are certain questions that although are local (if this...) you could still evaluate your Master Sketch and reach the correct answer, but you must have strong confidence, which you only get through lots of practice. But I would vote against this, most times if a question presents a condition, go ahead and make a mini diagram next to it.
Lets look at number 16. If U and Z appear together, exactly how money of the other friends must also appear?
Look at my diagram, its very clear that when U is in, S, W, and Y are all in, thats a tottal of 3 other variables, no reason to construct a mini sketch when my master diagram makes the solution very clear; , Z is attached to U, besides notice that the question states " how man of the other friends from Z and U.
I hope this helps.