Practice Exam 2 Maths Question #3

[mohit.wrangler]

Six billiard balls, numbered 1 through 6, are placed in a box. Three of the balls are red, and three are blue. One ball is to be drawn randomly from the box.

Quantity A
The probability that the ball drawn will be an even numbered red ball

Quantity B
1/2

--------------------------------------------------------------------------------------End of Question-------------------------------------------------------------------
Here is how I solved it:

P(drawn ball is even) = 1/2; P(the ball is red) = 1/2 -- Since it can be either red or blue i.e. given that three of the balls are red and other three are red => There is equal and uniform probability of each ball being read or blue => P(any ball being red) = 1/2

The probability that the ball drawn will be an even numbered red ball = 1/2 * 1/2 = 1/4

Second method:

The probability that the ball drawn will be an even numbered red ball = P(drawn ball is even) AND P(the drawn ball is red) => 1/2 * P(the drawn ball is red)

Since we know that since half of the balls are red and half of the balls are blue => 0< P(the drawn ball is red) <1

The probability that the ball drawn will be an even numbered red ball = 1/2 * X where 0<X<1

=>
The probability that the ball drawn will be an even numbered red ball IS AT LEAST <1/2 => B is the answer

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Where am I wrong?

[tommywallach]

You don't know which balls are red. It could be that all three of the red balls are ODD, in which case the odds of pulling one is 0. It could be that all three of the red balls are EVEN, in which case the odds of pulling one would be 1/2.

-t

P.S. Remember the GRE is as much a LOGIC test as it is a MATH test, so always make sure you've thought about a situation logically before you dive into creating equations.

[mohit.wrangler]

You don't know which balls are red. It could be that all three of the red balls are ODD, in which case the odds of pulling one is 0. It could be that all three of the red balls are EVEN, in which case the odds of pulling one would be 1/2.

-t

P.S. Remember the GRE is as much a LOGIC test as it is a MATH test, so always make sure you've thought about a situation logically before you dive into creating equations.

I understand your reasoning, and I agree completely. But, I want to clear my understanding.

Consider just this question: Six Billiard balls, marked numbers 1-6, are painted red or blue. Three of the balls are painted blue, and the rest three are painted red. What is the probability that the ball marked number 2 is painted red?


Sample space = 6C3 (assume this contains all possible set of 3 balls which are painted red; the other three becomes set of blue balls )
Consider 6C3 as
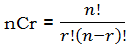
Favourable outcomes = 3 balls combination out of 5 balls (1, 3, 4, 5, 6) = 5C3 = 6C3 / 2 = # of ways set of three balls, containing ball #2, can be painted red
probability that the ball marked number 2 is painted red = Favourable outcomes / Sample space = 1/2
Or
Should I say, "It can't be calculated with the given information"?. Please mentioned the misassumption with above solution.

[tommywallach]

Hey Mohit,

Apologies, but you are wildly overthinking this. If half of the balls are blue and half are red, then obviously, any given ball has a 1/2 chance of being red and a 1/2 chance of being blue. No equations are required to answer that.

-t

[mohit.wrangler]

Hey Mohit,

Apologies, but you are wildly overthinking this. If half of the balls are blue and half are red, then obviously, any given ball has a 1/2 chance of being red and a 1/2 chance of being blue. No equations are required to answer that.

-t

Hi Tommy,

You can ignore my equations.
Now since you have answered this question, you can relate it back to the original question. Shouldn't your statement

any given ball has a 1/2 chance of being red and a 1/2 chance of being blue

applies to any random ball drawn from the box? If yes, the official answer can be challenged.

This is your reply from the previous post

You don't know which balls are red. It could be that all three of the red balls are ODD, in which case the odds of pulling one is 0. It could be that all three of the red balls are EVEN, in which case the odds of pulling one would be 1/2.

PS: This is my last post for this question. I promise.

[tommywallach]

You're acting as if your sample question is the same as the posed question, but it isn't. If we have 3 red balls and 3 blue balls, numbered 1-6, we can answer your posed question, but not the one from the original problem.

What are the odds of ANY ball being red: 1/2 (obviously)

What are the odds of an EVEN ball being red: No idea, because I don't know WHICH balls are red. Could be all of them, could be none of them.

Make sense now?

-t