Blast from the past! I first discussed the problems in this series way back in 2009. I’m reviving the series now because too many people just aren’t comfortable handling the weird maximize / minimize problem variations that the GMAT sometimes tosses at us.

In this installment, we’re going to tackle two GMATPrep® questions. Next time, I’ll give you a super hard one from our own archives—just to see whether you learned the material as well as you thought you did. 🙂

Here’s your first GMATPrep problem. Go for it!

“*Three boxes of supplies have an average (arithmetic mean) weight of 7 kilograms and a median weight of 9 kilograms. What is the maximum possible weight, in kilograms, of the lightest box?

“(A) 1

“(B) 2

“(C) 3

“(D) 4

“(E) 5”

When you see the word maximum (or a synonym), sit up and take notice. This one word is going to be the determining factor in setting up this problem efficiently right from the beginning. (The word minimum or a synonym would also apply.)

When you’re asked to maximize (or minimize) one thing, you are going to have one or more decision points throughout the problem in which you are going to have to maximize or minimize some other variables. Good decisions at these points will ultimately lead to the desired maximum (or minimum) quantity.

This time, they want to maximize the lightest box. Step back from the problem a sec and picture three boxes sitting in front of you. You’re about to ship them off to a friend. Wrap your head around the dilemma: if you want to maximize the lightest box, what should you do to the other two boxes?

Note also that the problem provides some constraints. There are three boxes and the median weight is 9 kg. No variability there: the middle box must weigh 9 kg.

The three items also have an average weight of 7. The total weight, then, must be (7)(3) = 21 kg.

Subtract the middle box from the total to get the combined weight of the heaviest and lightest boxes: 21 – 9 = 12 kg.

The heaviest box has to be equal to or greater than 9 (because it is to the right of the median). Likewise, the lightest box has to be equal to or smaller than 9. In order to maximize the weight of the lightest box, what should you do to the heaviest box?

Minimize the weight of the heaviest box in order to maximize the weight of the lightest box. The smallest possible weight for the heaviest box is 9.

If the heaviest box is minimized to 9, and the heaviest and lightest must add up to 12, then the maximum weight for the lightest box is 3.

The correct answer is (C).

Make sense? If you’ve got it, try this harder GMATPrep problem. Set your timer for 2 minutes!

“*A certain city with a population of 132,000 is to be divided into 11 voting districts, and no district is to have a population that is more than 10 percent greater than the population of any other district. What is the minimum possible population that the least populated district could have?

“(A) 10,700

“(B) 10,800

“(C) 10,900

“(D) 11,000

“(E) 11,100”

Hmm. There are 11 voting districts, each with some number of people. We’re asked to find the minimum possible population in the least populated district—that is, the smallest population that any one district could possibly have.

Let’s say that District 1 has the minimum population. Because all 11 districts have to add up to 132,000 people, you’d need to maximize the population in Districts 2 through 10. How? Now, you need more information from the problem:

“no district is to have a population that is more than 10 percent greater than the population of any other district”

So, if the smallest district has 100 people, then the largest district could have up to 10% more, or 110 people, but it can’t have any more than that. If the smallest district has 500 people, then the largest district could have up to 550 people but that’s it.

How can you use that to figure out how to split up the 132,000 people?

In the given problem, the number of people in the smallest district is unknown, so let’s call that x. If the smallest district is x, then calculate 10% and add that figure to x: x + 0.1x = 1.1x. The largest district could be 1.1x but can’t be any larger than that.

Since you need to maximize the 10 remaining districts, set all 10 districts equal to 1.1x. As a result, there are (1.1x)(10) = 11x people in the 10 maximized districts (Districts 2 through 10), as well as the original x people in the minimized district (District 1).

The problem indicated that all 11 districts add up to 132,000, so write that out mathematically:

11x + x = 132,000

12x = 132,000

x = 11,000

The correct answer is (D).

Practice this process with any max/min problems you’ve seen recently and join me next time, when we’ll tackle a super hard problem.

Key Takeaways for Max/Min Problems:

(1) Figure out what variables are “in play”: what can you manipulate in the problem? Some of those variables will need to be maximized and some minimized in order to get to the desired answer. Figure out which is which at each step along the way.

(2) Did you make a mistake—maximize when you should have minimized or vice versa? Go through the logic again, step by step, to figure out where you were led astray and why you should have done the opposite of what you did. (This is a good process in general whenever you make a mistake: figure out why you made the mistake you made, as well as how to do the work correctly next time.)

* GMATPrep® questions courtesy of the Graduate Management Admissions Council. Usage of this question does not imply endorsement by GMAC.

The newest GMAT Strategy Guides have hit the shelves! We’ve been working all year on updating our materials to give you the best and most up-to-date study materials possible.

What’s so great about the new books?

So many things, I don’t know where to start! Okay, let’s talk about quant first.

Every quant book contains between 1 and 3 entirely new chapters. These chapters are devoted to strategies that will help you solve quant problems more efficiently and more effectively. These strategies are a crucial reason why all of our teachers score in the 99^th percentile on the GMAT (I certainly wouldn’t consider taking the test without using them). We’ve always taught them in class and now we’re putting them in our books for the first time.

These strategies include:

Choosing Smart Numbers: you can turn certain algebra problems into arithmetic problems by substituting in your own numbers for the variables. We’re all better at arithmetic than we are at algebra, so you’ll definitely make your life easier (and be able to answer harder questions) by choosing smart numbers.

Testing Cases: On many data sufficiency problems (and even some problem solving problems), you’ll want to test cases in order to determine whether a statement is sufficient (or to eliminate wrong answers on PS). These problems are “theory” problems: the question may ask “Is n odd?” and then provide information that doesn’t allow you to determine a specific value for n, just whether specific characteristics are true of n.

Working Backwards: Sometimes, the problem is pretty annoying to set up and solve but the answers are all “nice” numbers: relatively small integers. In this case, you may be able to work backwards from the answers: pick one and try it in the problem to see whether it’s correct. The beauty of this technique: if you get good at it, on many problems you won’t have to try more than two answers in order to get to the correct one. I tested three answers on the solution in the article linked here, but I only really needed to test the first two; see if you can figure out why.

Estimation: Sometimes, the problem would be really irritating to solve exactly, but the answers are all decently spread apart. When this is the case, you can just estimate to solve! There are also a bunch of strategies for jumping between fractions, decimals, and percents to solve more quickly.

Combos: The GMAT likes to ask us to solve for a combination of variables, such as x + y. Sure, it’s possible that you may have to find x and y individually and then add them up, but it’s actually more likely that you’ll want to solve directly for that combo (x + y), especially on Data Sufficiency. Learn how to do this and also how to avoid DS traps in which the statement is not sufficient to solve for the individual variables but is sufficient to solve for the Combo.

Draw It Out: You can often solve the extra-annoying story problems, such as rates & work, via a “back of the envelope” approach: you sketch out a picture of the scenario and just “step” through it. For instance, you’d draw a timeline and map out exactly where those two trains are after 1 hour, 2 hours, 3 hours. It’s a little bit shocking how often this kind of strategy will get you all the way down to a single answer.

What is the best way to use the books?

I’ll leave you with a few tips about studying for quant. First, here’s the order that we use in our own classes:

1. Fractions, Decimals, & Percents
2. Algebra
3. Word Problems
4. Geometry
5. Number Properties

I actually think Number Properties is a more important topic than Geometry, but geo requires you to memorize a bunch of formulas; that takes some time, so we do it in class first. If you feel okay with that type of memorization, then do the Number Properties book first. (By the way, the Geometry Guide now contains a 1-page sheet with all of the important rules and formulas to memorize! Tear it right out and keep it handy for studying or use it to make flash cards for yourself.)

Next, I’d recommend starting with a few problems from the problem set at the end of the chapter—that’s right, before you even read the chapter! This creates curiosity, which really wakes your brain up and primes it to learn. Don’t do a bunch and don’t do the hardest ones (unless you think you’re really good at that topic). Just do about 2 or 3 problems and then dive into the chapter. (This will also help you to know how much time you’re likely going to want to spend on the chapter; if the problems are really a struggle, you may even want to review the equivalent chapter in our Foundations of Math Guide, if you have that book too.)

When you get to the end of the main chapters of that book, do the OG Mixed Questions Quiz that we’ve devised for you. (Certain longer books also have mid-way quizzes.) You can find these quizzes on our web site, where our Official Guide Problem Set study lists live. You’ll receive access to these problem sets and quizzes, along with other bonus materials, when you register your books on our site.

We moved the OG problem sets online because GMAC is going to start publishing new versions of their Official Guide books every year (in July, we’ve heard), so by moving the problem sets online, we’ve ensured that you’ll always be able to go and get the sets for the specific OG editions that you own.

I also have a ton of updates to share on the Verbal side as well, which are detailed in Part II. Also, a plea: if you get the new books, tell me what you think down in the comments. (Compliments or criticisms—I do want both.)

Visit our store and be the first to own the full set of our brand new Strategy Guides. Happy studying!

Studying for the GMAT? Take our free GMAT practice exam or sign up for a free GMAT trial class running all the time near you, or online. And, be sure to find us on Facebook and Google+,LinkedIn, and follow us on Twitter!

If you’re going to do a great job on Data Sufficiency, then you’ve got to know how to Test Cases. This strategy will help you on countless DS problems.

Try this GMATPrep® problem from the free exams. Give yourself about 2 minutes. Go!

* “On the number line, if the number k is to the left of the number t, is the product kt to the right of t?

“(1) t < 0 “(2) k < 1” If visualizing things helps you wrap your brain around the math (it certainly helps me), sketch out a number line:

k is somewhere to the left of t, but the two actual values could be anything. Both could be positive or both negative, or k could be negative and t positive. One of the two could even be zero.

The question asks whether kt is to the right of t. That is, is the product kt greater than t by itself?

There are a million possibilities for the values of k and t, so this question is what we call a theory question: are there certain characteristics of various numbers that would produce a consistent answer? Common characteristics tested on theory problems include positive, negative, zero, simple fractions, odds, evens, primes—basically, number properties.

“(1) t < 0 This problem appears to be testing positive and negative, since the statement specifies that one of the values must be negative. Test some real numbers, always making sure that t is negative.

Case #1:

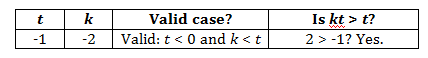
Testing Cases involves three consistent steps:

First, choose numbers to test in the problem

Second, make sure that you have selected a valid case. All of the givens must be true using your selected numbers.

Third, answer the question.

In this case, the answer is Yes. Now, your next strategy comes into play: try to prove the statement insufficient.

How? Ask yourself what numbers you could try that would give you the opposite answer. The first time, you got a Yes. Can you get a No?

Case #2:

Careful: this is where you might make a mistake. In trying to find the opposite case, you might try a mix of numbers that is invalid. Always make sure that you have a valid case before you actually try to answer the question. Discard case 2.

Case #3:

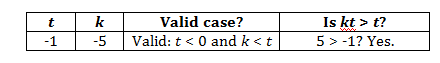
Hmm. We got another Yes answer. What does this mean? If you can’t come up with the opposite answer, see if you can understand why. According to this statement, t is always negative. Since k must be smaller than t, k will also always be negative.

The product kt, then, will be the product of two negative numbers, which is always positive. As a result, kt must always be larger than t, since kt is positive and t is negative.

Okay, statement (1) is sufficient. Cross off answers BCE and check out statement (2):

“(2) k < 1” You know the drill. Test cases again! Case #1:

You’ve got a No answer. Try to find a Yes.

Case #2:

Hmm. I got another No. What needs to happen to make kt > t? Remember what happened when you were testing statement (1): try making them both negative!

In fact, when you’re testing statement (2), see whether any of the cases you already tested for statement (1) are still valid for statement (2). If so, you can save yourself some work. Ideally, the below would be your path for statement (2), not what I first showed above:

“(2) k < 1” Case #1:

Now, try to find your opposite answer: can you get a No?All you have to do is make sure that the case is valid. If so, you’ve already done the math, so you know that the answer is the same (in this case, Yes).

Case #2: Try something I couldn’t try before. k could be positive or even 0…

A Yes and a No add up to an insufficient answer. Eliminate answer (D).

The correct answer is (A).

Guess what? The technique can also work on some Problem Solving problems. Try it out on the following GMATPrep problem, then join me next week to discuss the answer:

* “For which of the following functions f is f(x) = f(1 – x) for all x?

“(A) f(x) = 1 – x

“(B) f(x) = 1 – x²

“(C) f(x) = x² – (1 – x)²

“(D) f(x) = x²(1 – x)²

“(E) 

Key Takeaways: Test Cases on Data Sufficiency

(1) When DS asks you a “theory” question, test cases. Theory questions allow multiple possible scenarios, or cases. Your goal is to see whether the given information provides a consistent answer.

(2) Specifically, try to disprove the statement: if you can find one Yes and one No answer, then you’re done with that statement. You know it’s insufficient. If you keep trying different kinds of numbers but getting the same answer, see whether you can think through the theory to prove to yourself that the statement really does always work. (If you can’t, but the numbers you try keep giving you one consistent answer, just go ahead and assume that the statement is sufficient. If you’ve made a mistake, you can learn from it later.)

* GMATPrep® questions courtesy of the Graduate Management Admissions Council. Usage of this question does not imply endorsement by GMAC.

Studying for the GMAT? Take our free GMAT practice exam or sign up for a free GMAT trial class running all the time near you, or online. And, be sure to find us on Facebook and Google+,LinkedIn, and follow us on Twitter!

Memorize what? I’m not going to tell you yet. Try this problem from the GMATPrep® free practice tests first and see whether you can spot the most efficient solution.

All right, have you got an answer? How satisfied are you with your solution? If you did get an answer but you don’t feel as though you found an elegant solution, take some time to review the problem yourself before you keep reading.

Step 1: Glance Read Jot

Take a quick glance; what have you got? PS. A given equation, xy = 1. A seriously ugly-looking equation. Some fairly “nice” numbers in the answers. Hmm, maybe you should work backwards from the answers?

Jot the given info on the scrap paper.

Step 2: Reflect Organize

Oh, wait. Working backwards isn’t going to work—the answers don’t stand for just a simple variable.

Okay, what’s plan B? Does anything else jump out from the question stem?

Hey, those ugly exponents…there is one way in which they’re kind of nice. They’re both one of the three common special products. In general, when you see a special product, try rewriting the problem usually the other form of the special product.

Step 3: Work

Here’s the original expression again:

Let’s see.

Interesting. I like that for two reasons. First of all, a couple of those terms incorporate xy and the question stem told me that xy = 1, so maybe I’m heading in the right direction. Here’s what I’ve got now:

And that takes me to the second reason I like this: the two sets of exponents look awfully similar now, and they gave me a fraction to start. In general, we’re supposed to try to simplify fractions, and we do that by dividing stuff out.

How else can I write this to try to divide the similar stuff out? Wait, I’ve got it:

The numerator: 

The denominator: 

They’re almost identical! Both of the terms cancel out, as do the terms, leaving me with:

I like that a lot better than the crazy thing they started me with. Okay, how do I deal with this last step?

First, be really careful. Fractions + negative exponents = messy. In order to get rid of the negative exponent, take the reciprocal of the base:

Next, dividing by 1/2 is the same as multiplying by 2:

That multiplies to 16, so the correct answer is (D).

Key Takeaways: Special Products

(1) Your math skills have to be solid. If you don’t know how to manipulate exponents or how to simplify fractions, you’re going to get this problem wrong. If you struggle to remember any of the rules, start building and drilling flash cards. If you know the rules but make careless mistakes as you work, start writing down every step and pausing to think about where you’re going before you go there. Don’t just run through everything without thinking!

(2) You need to memorize the special products and you also need to know when and how to use them. The test writers LOVE to use special products to create a seemingly impossible question with a very elegant solution. Whenever you spot any form of a special product, write the problem down using both the original form and the other form. If you’re not sure which one will lead to the answer, try the other form first, the one they didn’t give you; this is more likely to lead to the correct answer (though not always).

(3) You may not see your way to the end after just the first step. That’s okay. Look for clues that indicate that you may be on the right track, such as xy being part of the other form. If you take a few steps and come up with something totally crazy or ridiculously hard, go back to the beginning and try the other path. Often, though, you’ll find the problem simplifying itself as you get several steps in.

* GMATPrep® questions courtesy of the Graduate Management Admissions Council. Usage of this question does not imply endorsement by GMAC.

Some Data Sufficiency questions present you with scenarios: stories that could play out in various complicated ways, depending on the statements. How do you get through these with a minimum of time and fuss?

Try the below problem. (Copyright: me! I was inspired by an OG problem; I’ll tell you which one at the end.)

* “During a week-long sale at a car dealership, the most number of cars sold on  any one day was 12. If at least 2 cars were sold each day, was the average daily number of cars sold during that week more than 6?

“(1) During that week, the second smallest number of cars sold on any one day was 4.

“(2) During that week, the median number of cars sold was 10.”

First, do you see why I described this as a “scenario” problem? All these different days… and some number of cars sold each day… and then they (I!) toss in average and median… and to top it all off, the problem asks for a range (more than 6). Sigh.

Okay, what do we do with this thing?

Because it’s Data Sufficiency, start by establishing the givens. Because it’s a scenario, Draw It Out.

Let’s see. The “highest” day was 12, but it doesn’t say which day of the week that was. So how can you draw this out?

Neither statement provides information about a specific day of the week, either. Rather, they provide information about the least number of sales and the median number of sales.

The use of median is interesting. How do you normally organize numbers when you’re dealing with median?

Bingo! Try organizing the number of sales from smallest to largest. Draw out 7 slots (one for each day) and add the information given in the question stem:

Now, what about that question? It asks not for the average, but whether the average number of daily sales for the week is more than 6. Does that give you any ideas for an approach to take?

Because it’s a yes/no question, you want to try to “prove” both yes and no for each statement. If you can show that a statement will give you both a yes and a no, then you know that statement is not sufficient. Try this out with statement 1

(1) During that week, the least number of cars sold on any one day was 4.

Draw out a version of the scenario that includes statement (1):

Can you find a way to make the average less than 6? Keep the first day at 2 and make the other days as small as possible:

The sum of the numbers is 34. The average is 34 / 7 = a little smaller than 5.

Can you also make the average greater than 6? Try making all the numbers as big as possible:

(Note: if you’re not sure whether the smallest day could be 4—the wording is a little weird—err on the cautious side and make it 3.)

You may be able to eyeball that and tell it will be greater than 6. If not, calculate: the sum is 67, so the average is just under 10.

Statement (1) is not sufficient because the average might be greater than or less than 6. Cross off answers (A) and (D).

Now, move to statement (2):

(2) During that week, the median number of cars sold was 10.

Again, draw out the scenario (using only the second statement this time!).

Can you make the average less than 6? Test the smallest numbers you can. The three lowest days could each be 2. Then, the next three days could each be 10.

The sum is 6 + 30 + 12 = 48. The average is 48 / 7 = just under 7, but bigger than 6. The numbers cannot be made any smaller—you have to have a minimum of 2 a day. Once you hit the median of 10 in the middle slot, you have to have something greater than or equal to the median for the remaining slots to the right.

The smallest possible average is still bigger than 6, so this statement is sufficient to answer the question. The correct answer is (B).

Oh, and the OG question is DS #121 from OG13. If you think you’ve got the concept, test yourself on the OG problem.

Key Takeaway: Draw Out Scenarios

(1) Sometimes, these scenarios are so elaborate that people are paralyzed. Pretend your boss just asked you to figure this out. What would you do? You’d just start drawing out possibilities till you figured it out.

(2) On Yes/No DS questions, try to get a Yes answer and a No answer. As soon as you do that, you can label the statement Not Sufficient and move on.

(3) After a while, you might have to go back to your boss and say, “Sorry, I can’t figure this out.” (Translation: you might have to give up and guess.) There isn’t a fantastic way to guess on this one, though I probably wouldn’t guess (E). The statements don’t look obviously helpful at first glance… which means probably at least one of them is!

So you’ve been told over and over that guessing is an important part of the GMAT. But knowing you’re supposed to guess and knowing when you’re supposed to guess are two very different things. Here are a few guidelines for how to decide when to guess.

But first, know that there are two kinds of guesses: random guesses and educated guesses. Both have their place on the GMAT. Random guesses are best for the questions that are so tough, that you don’t even know where to get started. Educated guesses, on the other hand, are useful when you’ve made at least some progress, but aren’t going to get all the way to an answer in time.

Here are a few different scenarios that should end in a guess.

Scenario 1: I’ve read the question twice, and I have no idea what it’s asking.

This one is pretty straightforward. Don’t worry about whether the question is objectively easy or difficult. If it’s too hard for you, it’s not worth doing. In fact, it’s so not worth doing that it’s not even worth your time narrowing down answer choices to make an educated guess. In fact, if it’s that difficult, it may even be better for you to get it wrong!

To make the most of your random guesses, you should use the same answer choice every time. The difference is slight, but it does up your odds of getting some of these random guess right.

Scenario 2: I had a plan, but I hit a wall.

Often, when this happens, you haven’t yet spent 2 minutes on the problem. So why guess? Maybe now you have a better plan for how to get to the answer. I know this is hard to hear, but don’t do it! To stay on pace for the entire section, you have to stay disciplined and that means that you only have one chance to get each question right.

The good news is that no 1 question you get wrong will kill your score. But, 1 question can really hurt your score if you spend too long on it! Once you realize that your plan didn’t work, it’s time to make an educated guess. You’ve already spent more than a minute on this question (hopefully not more than 2!), and you probably have some sense of which answers are more likely to be right. Take another 15 seconds (no more!) and make your best educated guess.

Scenario 3: I got an answer, but it doesn’t match any of the answer choices.

This is another painful one, but it’s an almost identical situation to Scenario 2. It means you either made a calculation error somewhere along the way, or you set the problem up incorrectly to begin with. In an untimed setting, both of these problems would have the same solution: go back over your work and find the mistake. On the GMAT, however, that process is too time-consuming. Plus, even once you find your mistake, you still have to redo all the work!

Once again, though it might hurt, it’s still in your best interest to let the question go. If you can narrow down the answer choices, great (though don’t spend longer than 15 or 20 seconds doing so). If not, don’t worry about it. Just make a random guess and vow to be more careful on the next one (and all the rest after that!).

Scenario 4: I checked my pacing chart and I’m more than 2 minutes behind.

Pacing problems are best dealt with early. If you’re more than 2 minutes behind, don’t wait until another 5 questions have passed and you realize you’re 5 minutes behind. At this point, you want to find a question in the next 5 that you can guess randomly on. The quicker you can identify a good candidate to skip, the more time you can make up.

This is another scenario where random guessing is best. Educated guessing takes time, and we’re trying to save as much time as possible. Look for questions that take a long time to read, or that deal with topics you’re not as strong in, but most importantly, just make the decision and pick up the time.

Wrap Up

Remember, this test is not like high school exams; it’s not designed to have every question answered. This test is about consistency on questions you know how to do. Knowing when to get out of a question is one of the most fundamental parts of a good score. The better you are at limiting time spent on really difficult questions, the more time you have to answer questions you know how to do.

Plan on taking the GMAT soon? We have the world’s best GMAT prep programs starting all the time. And, be sure to find us on Facebook and Google+, and follow us on Twitter!

Stop! Before you dive in and start calculating on a math problem, reflect for a moment. How can you set up the work to minimize the number of annoying calculations?

Try the below Percent problem from the free question set that comes with your GMATPrep® software. The problem itself isn’t super hard but the calculations can become time-consuming. If you find the problem easy, don’t dismiss it. Instead, ask yourself: how can you get to the answer with an absolute minimum of annoying calculations?

* ” The table above shows the results of a recent school board election in which the candidate with the higher total number of votes from the five districts was declared the winner. Which district had the greatest number of votes for the winner?

“(A) 1

“(B) 2

“(C) 3

“(D) 4

“(E) 5”

Ugh. We have to figure out what they’re talking about in the first place!

The first sentence of the problem describes the table. It shows 5 different districts with a number of votes, a percentage of votes for one candidate and a percentage of votes for a different candidate.

Hmm. So there were two candidates, P and Q, and the one who won the election received the most votes overall. The problem doesn’t say who that was. I could calculate that from the given data, but I’m not going to do so now! I’m only going to do that if I have to.

Let’s see. The problem then asks which district had the greatest number of votes for the winner. Ugh. I am going to have to figure out whether P or Q won. Let your annoyance guide you: is there a way to tell who won without actually calculating all the votes?

Read more

A couple of months ago, we talked about what to do when a geometry problem pops up on the screen. Do you remember the basic steps? Try to implement them on the below GMATPrep® problem from the free tests.

* ”In the xy-plane, what is the y-intercept of line L?

“(1) The slope of line L is 3 times its y-intercept
“(2) The x-intercept of line L is – 1/3”

My title (3 Steps to Better Geometry) is doing double-duty. First, here’s the general 3-step process for any quant problem, geometry included:

All geometry problems also have three standard strategies that fit into that process.

First, pick up your pen and start drawing! If they give you a diagram, redraw it on your scrap paper. If they don’t (as in the above problem), draw yourself a diagram anyway. This is part of your Glance-Read-Jot step.

Second, identify the “wanted” element and mark this element on your diagram. You’ll do this as part of the Glance-Read-Jot step, but do it last so that it leads you into the Reflect-Organize stage. Where am I trying to go? How can I get there?

Third, start Working! Infer from the given information. Geometry on the GMAT can be a bit like the proofs that we learned to do in high school. You’re given a couple of pieces of info to start and you have to figure out the 4 or 5 steps that will get you over to the answer, or what you’re trying to “prove.”

Let’s dive into this problem. They’re talking about a coordinate plane, so you know the first step: draw a coordinate plane on your scrap paper. The question indicates that there’s a line L, but you don’t know anything else about it, so you can’t actually draw it. You do know, though, that they want to know the y-intercept. What does that mean?

They want to know where line L crosses the y-axis. What are the possibilities?

Infinite, really. The line could slant up or down or it could be horizontal. In any of those cases, it could cross anywhere. In fact, the line could even be vertical, in which case it would either be right on the y-axis or it wouldn’t cross the y-axis at all. Hmm.
Read more

We invite you to test your GMAT knowledge for a chance to win! The second week of every month, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that month’s drawing for free Manhattan GMAT prep materials. Tell your friends to get out their scrap paper and start solving!

Here is this month’s problem:

If p, q, and r are different positive integers such that p + q + r = 6, what is the value of x ?

(1) The average of x^p and x^q is x^r.

(2) The average of x^p and x^r is not x^q.

Read more

What do you do when you realize a geometry problem has just popped up on the screen? Try this GMATPrep© problem from the free practice test and then we’ll talk about what to do!

In the figure above, the radius of the circle with center O is 1 and BC = 1. What is the area of triangular region ABC?

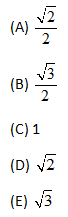
What’s your first step? Let’s use this problem as an opportunity to practice the Quant Process.

At a glance, you can see that the problem provides a diagram. Draw! Make it big enough that you can add labels as you calculate new pieces of information (and, of course, jot down any information given in the problem).

Finally, write down any formulas you’ll need, as well as whatever the problem asks you to find. Your scrap paper might look something like this:
Read more