Geometry – Who Said Geometry? It’s Algebra!
 The GMAT quant section has many faces – there are a number of content areas, and it is best to try to master as many of them as you can before test day. It is important, however, that you not compartmentalize too much. In many of the harder questions in fact, two or more topics often show up together. You can easily find quadratics in a consecutive integer question, coordinate geometry in a probability question, number properties in a function question, for example. One common intersection of two topics that I find surprises many students is that of geometry and algebra. Many people expect a geometry question to be about marking up diagrams with values or tick marks to show equality and/or applying properties and formulas to calculate or solve. While these are no doubt important skill sets in geometry, don’t forget to pull out one of the most important skills from your GMAT tool bag – the almighty variable! x’s and y’s have a welcomed home in many a geometry question, though you might find that you are the one who has to take the initiative to put them there!
The GMAT quant section has many faces – there are a number of content areas, and it is best to try to master as many of them as you can before test day. It is important, however, that you not compartmentalize too much. In many of the harder questions in fact, two or more topics often show up together. You can easily find quadratics in a consecutive integer question, coordinate geometry in a probability question, number properties in a function question, for example. One common intersection of two topics that I find surprises many students is that of geometry and algebra. Many people expect a geometry question to be about marking up diagrams with values or tick marks to show equality and/or applying properties and formulas to calculate or solve. While these are no doubt important skill sets in geometry, don’t forget to pull out one of the most important skills from your GMAT tool bag – the almighty variable! x’s and y’s have a welcomed home in many a geometry question, though you might find that you are the one who has to take the initiative to put them there!
Take a look at this data sufficiency question from GMATPrep®

In the figure shown, the measure of ![]() PRS is how many degrees greater than the measure of
PRS is how many degrees greater than the measure of ![]() PQR?
PQR?
(1) The measure of![]() QPR is 30 degrees.
QPR is 30 degrees.
(2) The sum of the measures of ![]() PQR and
PQR and ![]() PRQ is 150 degrees.
PRQ is 150 degrees.
How did you do? Don’t feel bad if you’re a little lost on this one. This is a difficult question, though you’ll see that with the right moves it is quite doable. At the end of this discussion, you’ll even see how you could put up a good guess on this one.
As is so often the case in a data sufficiency question, the right moves here start with the stem – in rephrasing the question. Unfortunately the stem doesn’t appear to provide us with a lot of given information. As indicated in the picture, you have a 90 degree angle at ![]() PQR and that seems like all that you are given, but it’s not! There are some other inherent RELATIONSHIPS, ones that are implied by the picture. For example
PQR and that seems like all that you are given, but it’s not! There are some other inherent RELATIONSHIPS, ones that are implied by the picture. For example ![]() PRS and
PRS and ![]() PRQ sum to 180 degrees. The problem, however, is how do you CAPTURE THOSE RELATIONSHIPS? The answer is simple – you capture those relationships the way you always capture relationships in math when the relationship is between two unknown quantities – you use variables!
PRQ sum to 180 degrees. The problem, however, is how do you CAPTURE THOSE RELATIONSHIPS? The answer is simple – you capture those relationships the way you always capture relationships in math when the relationship is between two unknown quantities – you use variables!
But where should you put the variables and how many variables should you use? This last question is one that you’ll likely find yourself pondering a number of times on the GMAT. Some believe the answer to be a matter of taste. My thoughts are always use as few variables as possible. If you can capture all of the relationships that you want to capture with one variable, great. If you need two variables, so be it. The use of three or more variables would be rather uncommon in a geometry question, though you could easily see that in a word problem. Keep one thing in mind when assigning variables: the more variables you use, usually the more equations you will need to write in order to solve.
As for the first question above about where to place the variables, you can take a closer look in this question at what they are asking and use that as a guide. They ask for the (degree) difference between ![]() PRS and
PRS and ![]() PQR. Since
PQR. Since ![]() PRS is in the question, start by labeling
PRS is in the question, start by labeling ![]() PRS as x. Since
PRS as x. Since ![]() PRS and
PRS and ![]() PRQ sum to 180 degrees, you can also label
PRQ sum to 180 degrees, you can also label ![]() PRQ as (180 – x) and
PRQ as (180 – x) and ![]() RPS as (180 – x – 90) or (90 – x).
RPS as (180 – x – 90) or (90 – x).
Can you continue to label the other angles in triangle PRQ in terms of x or is it now time to place a second variable, y? Since you still have two other unknown quantities in that triangle, it’s in fact time for that y. The logical place of where to put it is on ![]() PQR since that is also part of the actual question. The temptation is to stop there – DON’T! Continue to label the final angle of the triangle,
PQR since that is also part of the actual question. The temptation is to stop there – DON’T! Continue to label the final angle of the triangle, ![]() QPR, using your newfound companions, x and y.
QPR, using your newfound companions, x and y. ![]() QPR can be labeled as [180 – y – (180 – x)] or (x – y). Now all of the angles in the triangle are labeled and you are poised and ready to craft an algebraic equation/expression to capture any other relationships that might come your way.
QPR can be labeled as [180 – y – (180 – x)] or (x – y). Now all of the angles in the triangle are labeled and you are poised and ready to craft an algebraic equation/expression to capture any other relationships that might come your way.

Before you rush off to the statements, however, there is one last step. Formulate what the question is really asking in terms of x and y. The question rephrases to “What is the value of x – y?”
Now you can finally head to the statements. Oh the joy of a fully dissected data sufficiency stem – 90% of the work has already been done!
Statement (1) tells you that the measure of ![]() QPR is 30 degrees. Using your x – y expression from the newly labeled diagram as the value of
QPR is 30 degrees. Using your x – y expression from the newly labeled diagram as the value of ![]() QPR, you can jot down the equation x – y = 30. Mission accomplished! The statement is sufficient to answer the question “what is the value of x – y?”
QPR, you can jot down the equation x – y = 30. Mission accomplished! The statement is sufficient to answer the question “what is the value of x – y?”
Statement (2) indirectly provides the same information as statement (1). If the two other angles of triangle PQR sum to 150 degrees, then ![]() QPR is 30 degrees, so the statement is sufficient as well. If you somehow missed this inference and instead directly pulled from the diagram y + (180 – x) and set that equal to 150, you’d come to the same conclusion. Either way the algebra saves the day!
QPR is 30 degrees, so the statement is sufficient as well. If you somehow missed this inference and instead directly pulled from the diagram y + (180 – x) and set that equal to 150, you’d come to the same conclusion. Either way the algebra saves the day!
The answer to the question is D, EACH statement ALONE is sufficient to answer the question asked.
NOTE here that from a strategic guessing point of view, noticing that statements (1) and (2) essentially provide the same information allows you to eliminate answer choices A, B and C: A and B because how could it be one and not the other if they are the same, and C because there is nothing gained by combining them if they provide exactly the same information.
The takeaways from this question are as follows:
(1) When a geometry question has you staring at the diagram, uncertain of how to proceed in marking things up or capturing relationships that you know exist – use variables! Those variables will help you move through the relationships just as actual values would.
(2) In data sufficiency geometry questions, when possible represent the question in algebraic form so the target becomes clear and so that the rules of algebra are there to help you assess sufficiency.
(3) Once you have assigned a variable, continue to label as much of the diagram in terms of that variable. If you need a second variable to fully label the diagram, use it. If you can get away with just one variable and still accomplish the mission, do so.
Most GMAT test-takers know that they need to develop clear strategies when it comes to different types of word problems, and most of those involve either muscling your way through the problem with some kind of practical approach (picking numbers, visualizing, back-solving, logical reasoning) or writing out algebraic equations and solving. There are of course pluses and minuses to all of the approaches and those need to be weighed by each person on an individual basis. What few realize, however, is that geometry questions can also demonstrate that level of complexity and thus can often also be solved with the tools of algebra. When actual values are few and far between, don’t hesitate to pull out an “x” (and possibly also a “y”) and see what kind of equations/expressions you can cook up.
For more practice in “algebrating” a geometry question, please see OG 13th DS 79 and Quant Supplement 2nd editions PS 157, 162 and DS 60, 114 and 123.
The 4 Math Strategies Everyone Must Master, part 2
 Last time, we talked about the first 2 of 4 quant strategies that everyone must master: Test Cases and Choose Smart Numbers.
Last time, we talked about the first 2 of 4 quant strategies that everyone must master: Test Cases and Choose Smart Numbers.
Today, we’re going to cover the 3rd and 4th strategies. First up, we have Work Backwards. Let’s try a problem first: open up your Official Guide, 13th edition (OG13), and try problem solving #15 on page 192. (Give yourself about 2 minutes.)
I found this one by popping open my copy of OG13 and looking for a certain characteristic that meant I knew I could use the Work Backwards technique. Can you figure out how I knew, with just a quick glance, that this problem qualified for the Work Backwards strategy? (I’ll tell you at the end of the solution.)
For copyright reasons, I can’t reproduce the entire problem, but here’s a summary: John spends 1/2 his money on fruits and vegetables, 1/3 on meat, and 1/10 on treats from the bakery. He also spends $6 on candy. By the time he’s done, he’s spent all his money. The problem asks how much money he started out with in the first place.
Here are the answer choices:
“(A) $60
“(B) $80
“(C) $90
“(D) $120
“(E) $180”
Work Backwards literally means to start with the answers and do all of the math in the reverse order described in the problem. You’re essentially plugging the answers into the problem to see which one works. This strategy is very closely tied to the first two we discussed last time—except, in this instance, you’re not picking your own numbers. Instead, you’re using the numbers given in the answers.
In general, when using this technique, start with answer (B) or (D), your choice. If one looks like an easier number, start there. If (C) looks a lot easier than (B) or (D), start with (C) instead.
This time, the numbers are all equally “hard,” so start with answer (B). Here’s what you’re going to do:
(B) $80
|
|
F + V (1/2) |
M (1/3) |
B (1/10) |
C $6 |
Add? |
| (B) $80 |
$40 |
…? |
$6 |
Set up a table to calculate each piece. If John starts with $80, then he spends $40 on fruits and vegetables. He spends… wait a second! $80 doesn’t go into 1/3 in a way that would give a dollar-and-cents amount. It would be $26.66666 repeating forever. This can’t be the right answer!
Interesting. Cross off answer (B), and glance at the other answers. They’re all divisible by 3, so we can’t cross off any others for this same reason.
Try answer (D) next.
|
|
F + V (1/2) |
M (1/3) |
B (1/10) |
C $6 |
Add to? |
| (B) $80 |
$40 |
…? |
$6 |
? |
|
| (D) $120 |
$60 |
$40 |
$12 |
$6 |
$118 |
In order for (D) to be the correct answer, the individual calculations would have to add back up to $120, but they don’t. They add up to $118.
Okay, so (D) isn’t the correct answer either. Now what? Think about what you know so far. Answer (D) didn’t work, but the calculations also fell short—$118 wasn’t large enough to reach the starting point. As a result, try a smaller starting point next.
|
|
F + V (1/2) |
M (1/3) |
B (1/10) |
C $6 |
Add? |
| (B) $80 |
$40 |
…? |
$6 |
? |
|
| (D) $120 |
$60 |
$40 |
$12 |
$6 |
$118 |
| (C) $90 |
$45 |
$30 |
$9 |
$6 |
$90 |
It’s a match! The correct answer is (C).
Now, why would you want to do the problem this way, instead of the “straightforward,” normal math way? The textbook math solution on this one involves finding common denominators for three fractions—somewhat annoying but not horribly so. If you dislike manipulating fractions, or know that you’re more likely to make mistakes with that kind of math, then you may prefer to work backwards.
Note, though, that the above problem is a lower-numbered problem. On harder problems, this Work Backwards technique can become far easier than the textbook math. Try PS #203 in OG13. I would far rather Work Backwards on this problem than do the textbook math!
So, have you figured out how to tell, at a glance, that a problem might qualify for this strategy?
It has to do with the form of the answer choices. First, they need to be numeric. Second, the numbers should be what we consider “easy” numbers. These could be integers similar to the ones we saw in the above two problems. They could also be smaller “easy” fractions, such as 1/2, 1/3, 3/2, and so on.
Further, the question should ask about a single variable or unknown. If it asks for x, or for the amount of money that John had to start, then Work Backwards may be a great solution technique. If, on the other hand, the problem asks for x – y, or some other combination of unknowns, then the technique may not work as well.
(Drumroll, please) We’re now up to our fourth, and final, Quant Strategy that Everyone Must Master. Any guesses as to what it is? Try this GMATPrep© problem.

“In the figure above, the radius of the circle with center O is 1 and BC = 1. What is the area of triangular region ABC?
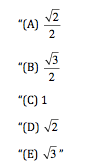
If the radius is 1, then the bottom line (the hypotenuse) of the triangle is 2. If you drop a line from point B to that bottom line, or base, you’ll have a height and can calculate the area of the triangle, since A = (1/2)bh.
You don’t know what that height is, yet, but you do know that it’s smaller than the length of BC. If BC were the height of the triangle, then the area would be A = (1/2)(2)(1) = 1. Because the height is smaller than BC, the area has to be smaller than 1. Eliminate answers (C), (D), and (E).
Now, decide whether you want to go through the effort of figuring out that height, so that you can calculate the precise area, or whether you’re fine with guessing between 2 answer choices. (Remember, unless you’re going for a top score on quant, you only have to answer about 60% of the questions correctly, so a 50/50 guess with about 30 seconds’ worth of work may be your best strategic move at this point on the test!)
The technique we just used to narrow down the answers is one I’m sure you’ve used before: Estimation. Everybody already knows to estimate when the problem asks you for an approximate answer. When else can (and should) you estimate?
Glance at the answers. Notice anything? They can be divided into 3 “categories” of numbers: less than 1, 1, and greater than 1.
Whenever you have a division like this (greater or less than 1, positive or negative, really big vs. really small), then you can estimate to get rid of some answers. In many cases, you can get rid of 3 and sometimes even all 4 wrong answers. Given the annoyingly complicated math that sometimes needs to take place in order to get to the final answer, your best decision just might be to narrow down to 2 answers quickly and then guess.
Want to know how to get to the actual answer for this problem, which is (B)? Take a look at the full solution here.
The 4 Quant Strategies Everyone Must Master
Here’s a summary of our four strategies.
(1) Test Cases.
– Especially useful on Data Sufficiency with variables / unknowns. Pick numbers that fit the constraints given and test the statement. That will give you a particular answer, either a value (on Value DS) or a yes or no (on Yes/No DS). Then test another case, choosing numbers that differ from the first set in a mathematically appropriate way (e.g., positive vs. negative, odd vs. even, integer vs. fraction). If you get an “always” answer (you keep getting the same value or you get always yes or always no), then the statement is sufficient. If you find a different answer (a different value, or a yes plus a no), then that statement is not sufficient.
– Also useful on “theory” Problem Solving questions, particularly ones that ask what must be true or could be true. Test the answers using your own real numbers and cross off any answers that don’t work with the given constraints. Keep testing, using different sets of numbers, till you have only one answer left (or you think you’ve spent too much time).
(2) Choose Smart Numbers.
– Used on Problem Solving questions that don’t require you to find something that must or could be true. In this case, you need to select just one set of numbers to work through the math in the problem, then pick the one answer that works.
– Look for variable expressions (no equals or inequalities signs) in the answer choices. Will also work with fraction or percent answers.
(3) Work Backwards.
– Used on Problem Solving questions with numerical answers. Most useful when the answers are “easy”—small integers, easy fractions, and so on—and the problem asks for a single variable. Instead of selecting your own numbers to try in the problem, use the given answer choices.
– Start with answer (B) or (D). If a choice doesn’t work, cross it off but examine the math to see whether you should try a larger or smaller choice next.
(4) Estimate.
– You’re likely already doing this whenever the problem actually asks you to find an approximate answer, but look for more opportunities to save yourself time and mental energy. When the answers are numerical and either very far apart or split across a “divide” (e.g., greater or less than 0, greater or less than 1), you can often estimate to get rid of 2 or 3 answers, sometimes even all 4 wrong answers.
The biggest takeaway here is very simple: these strategies are just as valid as any textbook math strategies you know, and they also require just as much practice as those textbook strategies. Make these techniques a part of your practice: master how and when to use them, and you will be well on your way to mastering the Quant portion of the GMAT!