Friday Links: Startups, Accredited MBAs, TED Talks, & More!
 Catch up on some business school news and tips with a few of this week’s top stories:
Catch up on some business school news and tips with a few of this week’s top stories:
Startups Recruiting More MBAs (Poets & Quants)
Startups are getting increased attention from MBAs and they’re apparently returning the love, according to a new survey.
Why Your MBA Should be Accredited (About.com Education)
If the degree or business school is not accredited, your achievements may not even be recognized by an employer.
14 of the Most Essential Lessons You Learn in Business School (Business Insider Australia)
Top business professors share which case studies they think are the most essential for future business leaders.
The Best TED Talks By B-School Professors (Poets & Quants)
Generally, the best TED talks by B-school faculty tend to be delivered by professors whose names are rarely mentioned outside their own schools.
Master the MBA Interview as an International Candidate (U.S. News Education)
Prospective students should anticipate making some mistakes when speaking English, but shouldn’t expect that to ruin the interview.
Did we miss your favorite article from the week? Let us know what you have been reading in the comments below or tweet @ManhattanGMAT
GMAT Challenge Problem Showdown: July 22, 2013

We invite you to test your GMAT knowledge for a chance to win! Each week, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that week’s drawing for a free Manhattan GMAT Prep item. Tell your friends to get out their scrap paper and start solving!
Here is this week’s problem:
In the xy-coordinate plane, line L passes through the points (b, a) and (c, 0), and line Mpasses through the point (a, b) and the origin, where a, b, and c are different nonzero integers. Do lines L and M intersect?
(1)
(2) c < 0
GMAT Percentiles Update
 Last week, GMAC updated its percentiles for GMAT scores. The organization does this once a year to smooth out any differences in the testing pool.
Last week, GMAC updated its percentiles for GMAT scores. The organization does this once a year to smooth out any differences in the testing pool.
What do I mean by “differences?” The demographics of the people taking the exam change over time. In particular, over the last ten years or so, GMAC has seen a huge increase in the number of non-United-States-based students taking the test. A majority of these students speak English as a second (or third!) language; a majority also have a better grounding in quantitative skills than the average U.S.-educated student. These differences lead to changes in the data over time.
Scaled Scores vs. Percentiles
GMAT results are reported using various “scaled scores.” We receive a 2-digit score for quant, a separate 2-digit score for verbal, a Q+V-combined 3-digit score, and two more separate scores for the essay and IR sections.
Think of these scaled scores as “skill levels.” They reflect a specific, measurable level of ability. Here’s the interesting thing: the skills needed to reach a certain level do not change over time. A quant score of 45 today reflects the same skill level as a quant score of 45 earned ten or even twenty years ago.
What does change over time is the percentile ranking associated with that score. A percentile ranking reflects how much better you did than a certain percentage of the test-taking population. For example, if you score in the 75th percentile, then you scored better than 75% of the people taking the test—not just that day, or that week, but for the past couple of years (or whatever timeframe is designated for that test).
Imagine that you give a math test to a bunch of 10-year-olds. The scoring algorithm is very simple: if you get a question right, you get one point. You then gather all of the scores and figure out percentile rankings for that group. Let’s say that a certain score (let’s call it 5) represents the 50th percentile. A student who scores 5 earned a better score than 50% of her peers.
Then you take that exact test and give it to a bunch of 14-year-olds. They’re a lot better at math. The same score of 5 might represent only the 25th percentile for this new group, because more of these students have better math skills and can answer more questions correctly. A score of 5 still means the same thing (in this case, 5 questions right), but the pool of testers has changed and so the percentile rankings change too.
This is essentially what happens with the GMAT over time as well. If more people who are good at math start taking the test, then that score of 45 (which represents a certain, fixed level of skill) will drop in the percentile rankings because more people will be capable of performing at that level or higher.
We’ve seen especially big demographic changes on the GMAT over the last 5 to 10 years. In 2006, a quant score of 45 was rated the 78th percentile. Someone scoring at that level had better quant skills than 78% of the people taking the exam around that time.
Today, that same skill level of 45 rates the 66th percentile. This does not mean that someone scoring a 45 today is worse at math than someone with the same score in 2006; rather, the two students are equally good. Instead, a greater percentage of the population taking the test today has stronger math skills.
You might be thinking: oh, great. So that means I have to do even better at math. Actually, the opposite is (sort of) true. Keep reading.
This Year’s Trends
The Second Level of Learning to Take the GMAT
 You already know how to learn—you’ve been learning all your life. The problem is that the way you learn best for school is often not the best way of learning to take the GMAT. Read more
You already know how to learn—you’ve been learning all your life. The problem is that the way you learn best for school is often not the best way of learning to take the GMAT. Read more
Free GMAT Events This Week: July 22 – July 28
Here are the free GMAT events we’re holding this week. All times are local unless otherwise specified.
7/22/13– Chicago, IL – Free Trial Class– 6:30PM- 9:30PM
7/22/13– Boston, MA- Assessing Your MBA Profile presented by mbaMission– 7:00PM- 8:30PM
7/22/13– Austin, TX- Free Trial Class– 6:30PM- 9:30PM
7/23/13– Online – Live Online GMAT Preview– 8:00PM- 9:30PM (EDT)
7/23/13– New York, NY – Writing a Standout HBS Application Essay presented by mbaMission– 7:00PM- 8:30PM
7/24/13– Santa Monica, CA – Free Trial Class– 6:30PM- 9:30PM
7/24/13– Toronto, ON- Free Trial Class– 6:30PM- 9:30PM
7/25/13– Online – Free Trial Class– 9:00PM- 12:00PM (EDT)
7/25/13– Boston, MA- Free Trial Class– 6:30PM- 9:30PM
Read more
Friday Links: Wharton’s GMAT Record, Leadership Lessons, &More!
 Catch up on some business school news and tips with a few of this week’s top stories:
Catch up on some business school news and tips with a few of this week’s top stories:
Wharton’s Record GMATs for New Class (Poets and Quants)
Despite a 5.8% fall in MBA applications, Wharton said it has enrolled a larger first-year class of 855 with an average GMAT score that is seven points higher at 725.
The World’s Best Business Schools (Business Insider)
Having an MBA can give you an edge in the cutthroat world of business—but only if you pick the right school.
Leadership Lessons from The Harvard of Europe (Forbes)
Associate Dean at HEC Paris talks about how leadership is far more about being knowledgeable and gaining respect than being able to do a good presentation in the boardroom.
Cornell To Offer One-Year MBA in NYC (Poets and Quants)
The Johnson Graduate School of Management at Cornell University will soon offer a one-year MBA program based at Google’s New York City campus.
MBA Teaching urged to move away from focus on shareholder primacy model (Financial Times)
Academics and others are being increasingly vocal about how deeply entrenched the idea of shareholder primacy is in management.
Did we miss your favorite article from the week? Let us know what you have been reading in the comments below or tweet @ManhattanGMAT
Paranoia Runs Deep, Into Your Heart It Will Creep
I know what Statement 2 is telling me; it’s saying ˜Become a carpenter!’
Why is this question here? Why am I here? When’s the civil service exam? Garbage men still have a union. . .
 Have you lived that movie? Paranoia is only human and the old saying is true: Just because you’re paranoid doesn’t mean they’re not out to get you. Paranoia is a primal reaction, developed to help protect humans from animals with sharp, pointy teeth. Unfortunately, it is not helpful when one is facing questions with sharp, pointy teeth. Even though the GMAT is out to get you. Failing to control your paranoia is a hidden reason for underperforming on the actual exam.
Have you lived that movie? Paranoia is only human and the old saying is true: Just because you’re paranoid doesn’t mean they’re not out to get you. Paranoia is a primal reaction, developed to help protect humans from animals with sharp, pointy teeth. Unfortunately, it is not helpful when one is facing questions with sharp, pointy teeth. Even though the GMAT is out to get you. Failing to control your paranoia is a hidden reason for underperforming on the actual exam.
On this blog, I and others have discussed many factors crucial for success: foundation skills, strategies, timing, precision, and so forth. And it’s like I say about L.A.—everything you ever read [here] about it is true. However, after honing these skills, after achieving mastery, too many test takers succumb to their paranoia and thus revert when taking the actual exam, especially for the first time. Even 99th percentile skills will crumble if undermined by irrational panic and the results will not be gratifying. (Have you ever watched the Chicago Cubs play a post season series?) To succeed, folks must understand the difference between dispassionate, objective analysis—I’ve never gotten a combinatrics question right in life, why do I think I’ll have a divine inspiration today?—and irrelevant fear—They’re going to tattoo a scarlet L on my forehead. Just as folks plan question and timing strategies, they must develop tools to banish their internally generated negative visualizations.
How do you tell the difference? Objective analysis responds to the stimuli on the monitor. Paranoia is a response to internal doubts. (Notice how this is parallel to the nature of the exam—search for the answer on the screen, not in the opinions in your head.) Sometimes, after you’ve read a question twice (everyone has a sinking feeling the first time), you hear yourself singing, I’ve got the ˜I don’t know where I’m going but I’m going nowhere in a hurry’ blues. That’s the truth, not paranoia. Bail out. As one of my acting coaches used to say, Only schizophrenics don’t react to the reality around them. Conversely, paranoia is when your thoughts of impending disaster revolve around your supposed shortcomings rather than the material on the screen. As I’ve said before, if while taking the exam you find yourself thinking about how big a dumb ass you are, check the question—if it doesn’t read, Which of the following best describes how big a dumb ass you are?, you’re thinking about the wrong thing. That is paranoia. No kidding—you knew that.
Well then, why do people recognize the difference between analysis and paranoia but still succumb to the latter? Because they try to do the impossible. They try not to have thoughts of failure. That’s impossible—you can’t override human nature. I have feelings of paranoia, even though I’ve always scored in the 99th percentile. I still have them”even though I don’t really care about my score anymore. Instead, you have to recognize irrationality in yourself and laugh it off. I say to myself, Save some of that craziness for menopause. Then I giggle, read the question again, and really listen to the words. And if I still don’t get it, I say, Screw them if they can’t take a joke. And bail out.
Maybe some of you can’t make jokes to yourself during the exam because you’re worried about your entire future. That’s part of the problem—if a chunk (or all) of your mind is thinking about things other than the words on the monitor, it will lower your score. It’s the difference between worrying about being the hero or the goat and just seeing the ball and hitting the ball. Feelings of failure while taking the exam are like stage fright. That’s what stage fright is—standing up there thinking you look like an idiot. You say, No, it’s much different—they give me a piece of paper that says I’m an idiot. No. Really. It’s the same. So, I’ve got another suggestion for you, if you didn’t like the first one.
Remainders – Who Needs Them Anyway??
 We were taught in school to think of whole numbers in the context of two groups: Odds vs. Evens. I remember thinking it was like the black vs. white pieces on a chess board (I was kind of a nerd). As I’m sure you know, an Even number is simply a number divisible by 2, and an Odd number is any number that’s not even. But ask yourself this: what is the remainder when you divide an odd number by 2? Take a minute to think about this. Try out a few different odd numbers and see if you can identify a pattern.
We were taught in school to think of whole numbers in the context of two groups: Odds vs. Evens. I remember thinking it was like the black vs. white pieces on a chess board (I was kind of a nerd). As I’m sure you know, an Even number is simply a number divisible by 2, and an Odd number is any number that’s not even. But ask yourself this: what is the remainder when you divide an odd number by 2? Take a minute to think about this. Try out a few different odd numbers and see if you can identify a pattern.
The remainder will always be 1 when you divide an odd number by 2. Always. And when you divide an even number by 2? Well, by definition the even number is divisible by 2, so the remainder is therefore zero.
The GMAT loves taking this concept and testing how deep your understanding goes. Therefore, we must free ourselves of the simplistic odd vs. even framework that we were fed in school, and explore this concept to a much deeper level. That is exactly what I intend to do in this blog post.
I always joke with my students that if I were the number 3 on the number line, I would really hate my next door neighbor to the left (number 2). He thinks he’s so special because there’s a name for any multiple of him (“even”); and if that’s not enough to give him a big head, they also invented a name for any number that isn’t a multiple of him (“odd”). What do you call multiples of me? “multiple of 3”. What do you call numbers that are not multiples of me? “not a multiple of 3”. LAME
Another Way To Solve Median & Mean Questions
 This is the second of a series of posts that offer alternate ways to solve certain GMAT problems (check out the first here: DS Value Problems). Just like last time, if you like the method, steal it! And if you don’t, I promise not to lose any sleep. There’s a lot of ways to solve most questions on the GMAT and the best way will always be the way that works best for you. So without further ado, let’s check out a GMATPrep question and see how fast you can solve:
This is the second of a series of posts that offer alternate ways to solve certain GMAT problems (check out the first here: DS Value Problems). Just like last time, if you like the method, steal it! And if you don’t, I promise not to lose any sleep. There’s a lot of ways to solve most questions on the GMAT and the best way will always be the way that works best for you. So without further ado, let’s check out a GMATPrep question and see how fast you can solve:
Last month 15 homes were sold in Town X. The average (arithmetic mean) sale price of the homes was $150,000 and the median sale price was $130,000. Which of the following statements must be true?
I. At least one of the homes was sold for more than $165,000.
II. At least one of the homes was sold for more than $130,000 and less than $150,000.
III. At least one of the homes was sold for less than $130,000.
(A) I only
(B) II only
(C) III only
(D) I and II
(E) I and III
First things first, if you answered this question using algebra, you’re in great company. Another one of our instructors, Stacey Koprince, has a great write up on the algebra in this question, and it’s definitely worth a read-through right here. But a lot of questions on the GMAT, including this one, can be solved by thinking of extremely simple scenarios, rather than the algebra that determines all of them.
The first thing I noticed on this question is that this is one of those awful questions where there’s a whole lot of wiggle room with the information that they give you. What was the cheapest house? What was the cost of the third most expensive house? Were any of the houses all the same price? If the second cheapest house is half as expensive as the most expensive, how does that affect the cost of the other houses? It’s easy to get lost when you start to think about how little you know in this scenario.
But before I jump around and start picking values out of thin air, the most important part of this problem are the (few) things that MUST be true. In this case, there are two: the 15 house prices have a mean of $150,000 and a median of $130,000. And on my paper, I would write out a few slots to represent the house prices like this: (note- I wouldn’t write out all 15 slots. Just the first few, the last few, and, since this is a median problem, one in the middle.)
|
____ |
____ |
… |
____ |
… |
____ |
____ |
|
1 |
2 |
7 |
14 |
15 |
Again, there are two things that they tell me here, but I want to start with the most restrictive element in this problem. There are lots of different ways to get a mean of $150,000, but in order to get a median of $130,000, I would need at least one house to cost EXACTLY $130,000. So I add that to my chart (ignoring the $ sign and extra zeroes):
GMAT Challenge Problem Showdown: July 15, 2013

We invite you to test your GMAT knowledge for a chance to win! Each week, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that week’s drawing for a free Manhattan GMAT Prep item. Tell your friends to get out their scrap paper and start solving!
Here is this week’s problem:
If n is a positive integer greater than 1, what is the smallest positive difference between two different factors of n?
(1)
is a positive integer.
(2) n is a multiple of both 11 and 9.
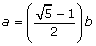
 is a positive integer.
is a positive integer.