GMAT Challenge Problem Showdown: May 27, 2013
We invite you to test your GMAT knowledge for a chance to win! Each week, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that week’s drawing for a free Manhattan GMAT Prep item. Tell your friends to get out their scrap paper and start solving!
Here is this week’s problem:
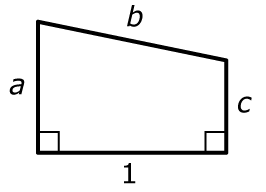
In the trapezoid above, with sides a, b, c, and 1, what is the value of ac ?
(1) a + c = b
(2) a “ c = 1
Want a 750+? Think Your Way Through This Challenge Problem!
A few months ago, I wrote a couple of articles targeted toward those students looking for a super-high score (one for quant, one for verbal). I challenged students to answer those questions in much less time than we typically average on test questions.
Well, I’m back with another one in the series. This problem is a bit different though: it’s from our Challenge Problem archive, a question bank consisting of what we call 800+ level problems. (Some might qualify as 750+ but most are harder than anything you’ll ever see on the real test.)
Do you need to be able to answer a question like this in order to score 750+? Absolutely not. (In fact, after my colleague Ron Purewal submitted this question, I tested it out on several of my fellow instructors, all of whom have scored 760+ on the test. Not everyone answered correctly.) Mostly, I’m offering this to stretch your brains, drive you a little crazy, and make one important point (see my second takeaway at the end).
If, however, quant is your strength and you’re hoping to score 51 in that section”you can certainly score 51 without getting this one right, but if you do get this one right in 2 minutes, then you know you’re ready for the quant section.
One more tidbit before we dive in. I chose this question because it is SO very hard. As of right now (as I’m typing this), 254 people have tried this problem and 44 have answered it correctly.
Do a little math here. What percentage of people answered the question correctly?
17%. Random guess position is 20%. Wow.
GMAT Challenge Problem Showdown: May 20, 2013
We invite you to test your GMAT knowledge for a chance to win! Each week, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that week’s drawing for a free Manhattan GMAT Prep item. Tell your friends to get out their scrap paper and start solving!
Here is this week’s problem:
The octagon in the diagram above is regular: all of its sides are of equal length, and all of its angles are of equal measure. If the octagon’s perimeter is 8 inches, and every other vertex of the octagon is connected to create a square as shown above, what is the area of the square?
Another Way to Solve Data Sufficiency Value Problems, The Goldilocks Method, & Finding a Number That’s Just Right
One of the hardest parts about becoming an instructor with Manhattan GMAT was relearning how to solve GMAT questions. That sounds absurd, considering I had already scored a 780 on the GMAT when I applied to become an instructor, but it’s true. During the interview process, I went through online and in-person classroom simulations with 99th percentile instructors playing students, testing my ability to explain a question using algebra instead of plugging numbers or using a rate chart instead of adding rates. Over the years, I’ve found that many of our instructors felt the same way: overwhelmed by how hard it is to go along with someone else’s preferred method without skipping a beat. Ultimately, I realized that teaching the GMAT is a hundred times harder than taking the GMAT because every question has several valid ways of being solved.
Which leads to the problem of what solution is the BEST solution. Any student who has worked with me over the years has heard me say the following- I don’t care what method you use to solve a problem. But I do care that you get great at that method. It’s the reason why the Official Guide has an explanation for each quant problem and Manhattan has an OG Companion with different explanations, along with online video explanations that will sometimes differ from either of those methods. With so many different ways of solving a question, it’s important to not get bogged down finding the best way to solve a problem, but instead focus on finding the fastest way from start to submit.
So with that said, over the next few months, I’d like to share a few methods that I personally use when solving a few different types of GMAT questions. Some of these methods might click for you, and I hope you practice them. Some of them won’t and I hope you stick with a method that works better for you. So without further ado- let’s take a look at a fairly straightforward GMATPrep problem and think about how you would attack this question:
A sum of $200,000 from a certain estate was divided among a spouse and three children. How much of the estate did the youngest child receive?
(1) The spouse received 1/2 of the sum from the estate, and the oldest child received 1/4 of the remainder.
(2) Each of the two younger children received $12,500 more than the oldest child and $62,500 less than the spouse.
The first two things that I notice about this problem is that it is a word problem, giving us a real-world scenario, and a value Data Sufficiency question, asking us to find a single value for the amount that the youngest child received. And if I wanted to set this up algebraically, I could assign variables (s = spouse, x, y, z = oldest, middle, youngest child), write out several equations (s + x + y + z = 200,000. (1) s = 1/2*200,000; x = 1/4 * (1/2*200,000); y + z = 75,000. (2) y = z; z = x + 12,500; z = s − 62,500), and eventually solve for z using Statement 2: the correct answer is (B). Different students at different levels of comfort with Data Sufficiency will be able to stop at different points after realizing that there either will or will not be a single variable in the equation that they’ve set up.
GMAT Challenge Problem Showdown: May 13, 2013
We invite you to test your GMAT knowledge for a chance to win! Each week, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that week’s drawing for a free Manhattan GMAT Prep item. Tell your friends to get out their scrap paper and start solving!
Here is this week’s problem:
If 5a + 7b = k, where a and b are positive integers, what is the largest possible value of k for which exactly one pair of integers (a, b) makes the equation true?
GMAT Challenge Problem Showdown: May 6, 2013
We invite you to test your GMAT knowledge for a chance to win! Each week, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that week’s drawing for a free Manhattan GMAT Prep item. Tell your friends to get out their scrap paper and start solving!
Here is this week’s problem:
The length and width of a rectangle are integer values. What is the area of the smallest such rectangle that can be inscribed in a circle whose radius is also an integer?
Challenge Problem Showdown- April 29, 2013
We invite you to test your GMAT knowledge for a chance to win! Each week, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that week’s drawing for a free Manhattan GMAT Prep item. Tell your friends to get out their scrap paper and start solving!
Here is this week’s problem:
In a certain type of tiling called Penrose P3 tiling, two types of rhombi fill a space without gaps or overlaps: wide rhombi and narrow rhombi. If five of the wide rhombi can meet symmetrically at a single point, while ten of the narrow rhombi can, what is the ratio of the largest angle in one narrow rhombus to the largest angle in one wide rhombus?
Challenge Problem Showdown- April 22, 2013
We invite you to test your GMAT knowledge for a chance to win! Each week, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that week’s drawing for a free Manhattan GMAT Prep item. Tell your friends to get out their scrap paper and start solving!
Here is this week’s problem:
If x is positive, what is the value of |x “ 3| “ 2|x “ 4| + 2|x “ 6| “ |x “ 7| ?
(1) x is an odd integer.
(2) x > 6
Challenge Problem Showdown- April 15, 2013
We invite you to test your GMAT knowledge for a chance to win! Each week, we will post a new Challenge Problem for you to attempt. If you submit the correct answer, you will be entered into that week’s drawing for a free Manhattan GMAT Prep item. Tell your friends to get out their scrap paper and start solving!
Here is this week’s problem:
The value of investment Q increased by q percent from the beginning of a particular year through June 30 of that year, and then experienced no net change from June 30 to the end of the year. The value of investment P increased by p percent from the beginning of that year to June 30, and the new value increased again by p percent from June 30 to the end of the year. If the percent increase in value from the beginning to the end of the year was the same for both investments, which of the following expressions gives the value of p in terms of q?
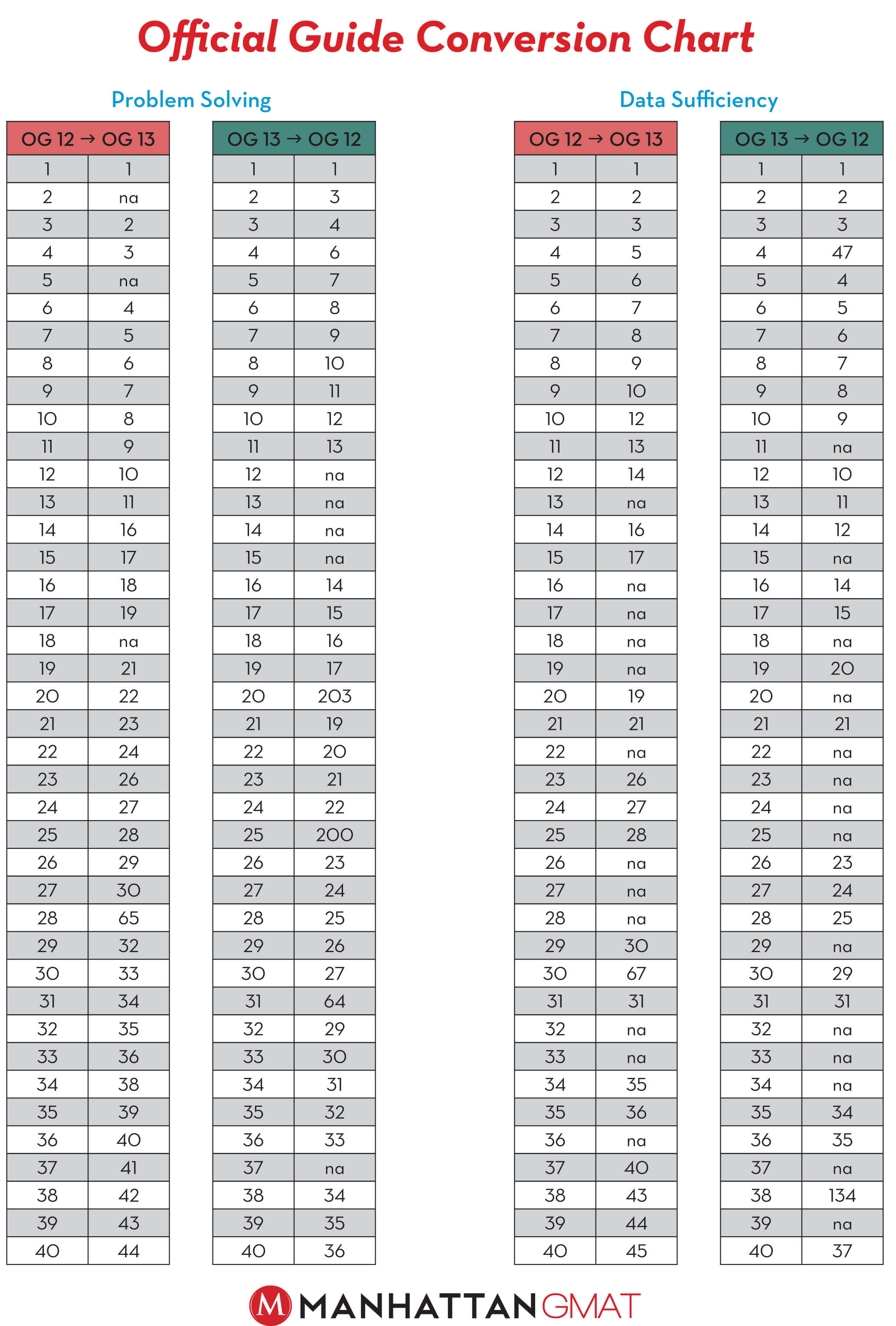
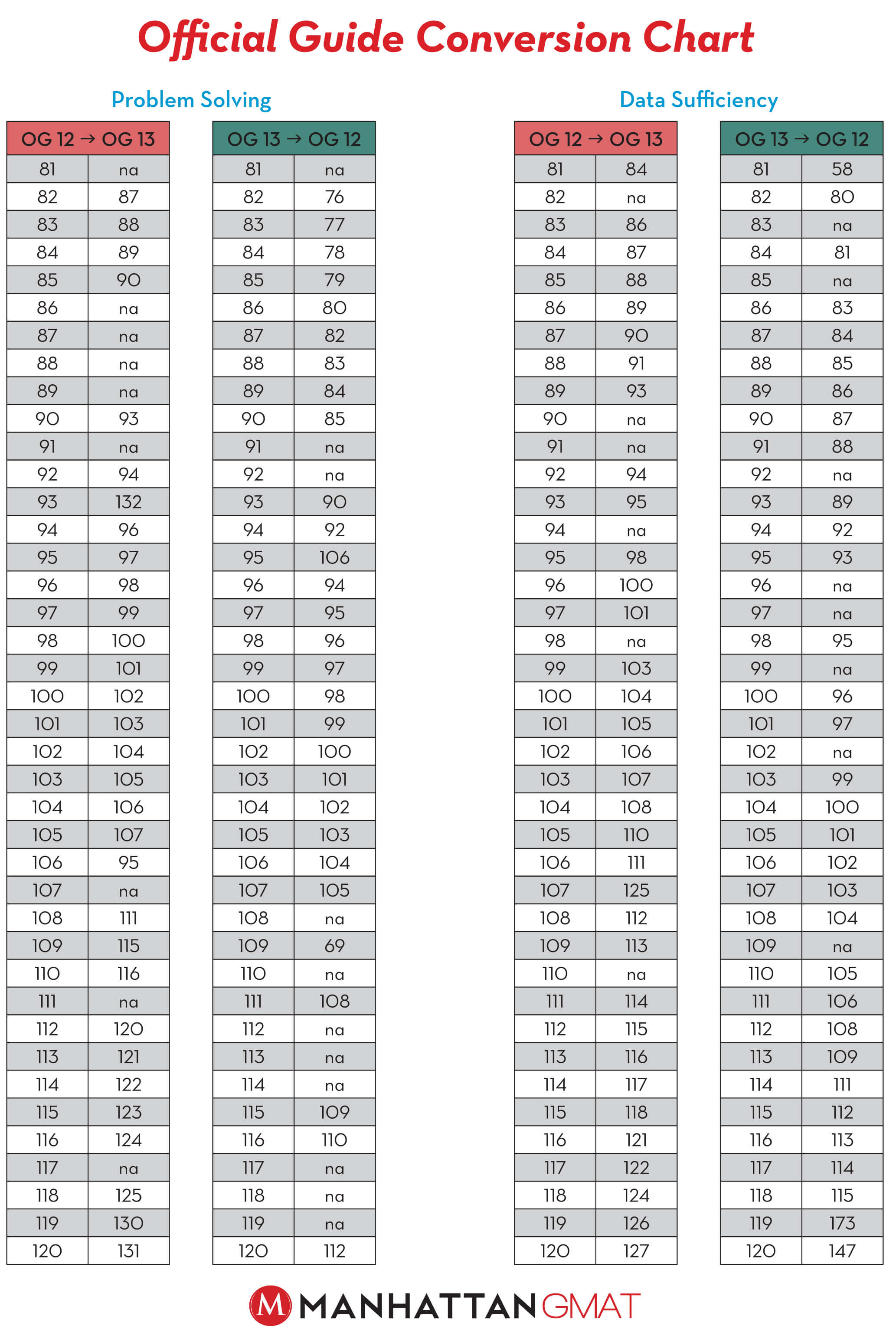
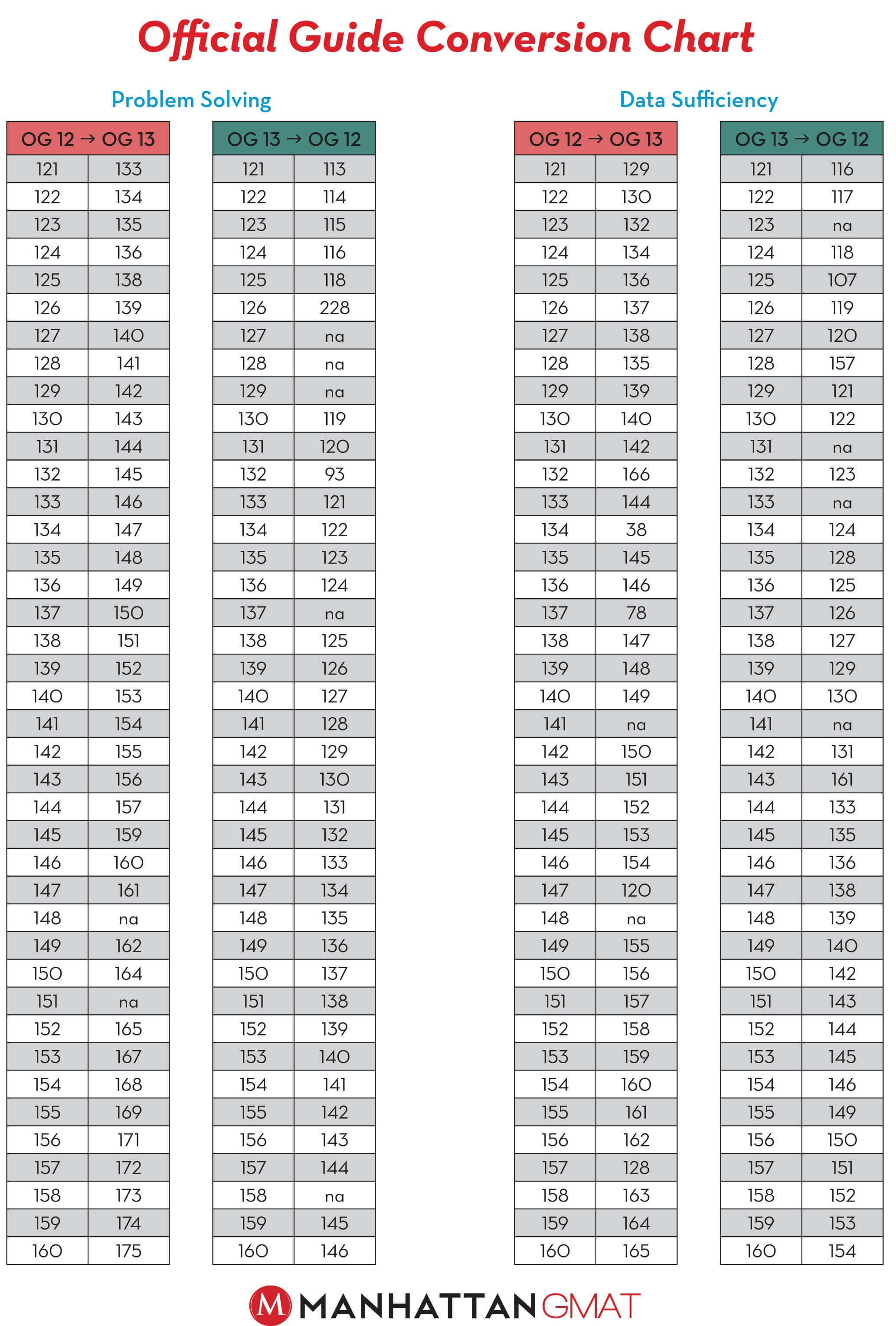
OG 13 Conversion Guide – Quant
Need to convert your Official Guide 12 problems to OG13 problems? Or visa versa? Check out our hand-dandy conversion guide for Quant problems, below. You can find our conversion guide for Verbal problems here.
