3 Steps to Better Geometry
 A couple of months ago, we talked about what to do when a geometry problem pops up on the screen. Do you remember the basic steps? Try to implement them on the below GMATPrep® problem from the free tests.
A couple of months ago, we talked about what to do when a geometry problem pops up on the screen. Do you remember the basic steps? Try to implement them on the below GMATPrep® problem from the free tests.
* ”In the xy-plane, what is the y-intercept of line L?
“(1) The slope of line L is 3 times its y-intercept
“(2) The x-intercept of line L is – 1/3”
My title (3 Steps to Better Geometry) is doing double-duty. First, here’s the general 3-step process for any quant problem, geometry included:

All geometry problems also have three standard strategies that fit into that process.
First, pick up your pen and start drawing! If they give you a diagram, redraw it on your scrap paper. If they don’t (as in the above problem), draw yourself a diagram anyway. This is part of your Glance-Read-Jot step.
Second, identify the “wanted” element and mark this element on your diagram. You’ll do this as part of the Glance-Read-Jot step, but do it last so that it leads you into the Reflect-Organize stage. Where am I trying to go? How can I get there?
Third, start Working! Infer from the given information. Geometry on the GMAT can be a bit like the proofs that we learned to do in high school. You’re given a couple of pieces of info to start and you have to figure out the 4 or 5 steps that will get you over to the answer, or what you’re trying to “prove.”
Let’s dive into this problem. They’re talking about a coordinate plane, so you know the first step: draw a coordinate plane on your scrap paper. The question indicates that there’s a line L, but you don’t know anything else about it, so you can’t actually draw it. You do know, though, that they want to know the y-intercept. What does that mean?
They want to know where line L crosses the y-axis. What are the possibilities?
Infinite, really. The line could slant up or down or it could be horizontal. In any of those cases, it could cross anywhere. In fact, the line could even be vertical, in which case it would either be right on the y-axis or it wouldn’t cross the y-axis at all. Hmm.
Read more
Want a 51 on Quant? Can you answer this problem?
 Sequence problems aren’t incredibly common on the test, but if you’re doing well on the quant section, be prepared to see one. Now, you’ve got a choice: do you want to guess quickly and save time for other, easier topics? Do you want to learn some “test savvy” techniques that will help you with some sequence questions but possibly not all of them? Or do you want to learn how to do these every single time, no matter what?
Sequence problems aren’t incredibly common on the test, but if you’re doing well on the quant section, be prepared to see one. Now, you’ve got a choice: do you want to guess quickly and save time for other, easier topics? Do you want to learn some “test savvy” techniques that will help you with some sequence questions but possibly not all of them? Or do you want to learn how to do these every single time, no matter what?
That isn’t a trick question. Every good business person knows that there’s a point of diminishing returns: if you don’t actually need a 51, then you may study for a lower (but still good!) score and re-allocate your valuable time elsewhere.
Try this GMATPrep® problem from the free test. After, we’ll talk about how to do it in the “textbook” way and in the “back of the envelope” way.
* ”For every integer k from 1 to 10, inclusive, the kth term of a certain sequence is given by ![]() . If T is the sum of the first 10 terms in the sequence, then T is
. If T is the sum of the first 10 terms in the sequence, then T is
“(A) greater than 2
“(B) between 1 and 2
“(C) between 1/2 and 1
“(D) between 1/4 and 1/2
“(E) less than 1/4”
First, let’s talk about how to do this thing in the “textbook math” way. If you don’t want to do this the textbook math way, feel free to skip to the second method below.
Textbook Method
If you’ve really studied sequences, then you may recognize the sequence as a particular kind called a Geometric Progression. If not, you would start to find the terms and see whether you can spot a pattern.
Plug in k = 1, 2, 3. What’s going on?

What’s going on here? Each time, the term gets multiplied by -1/2 in order to get to the next one. When you keep multiplying by the same number in order to get to the next term, then you have a geometric progression.
This next part gets into some serious math. Unless you really just love math, I wouldn’t bother learning this part for the GMAT, because there’s a very good chance you’ll never need to use it. But, if you want to, go for it!
When you have a geometric progression, you can calculate the sum in the following way:
![]()
Next, you’re going to multiply every term in the sum by the common ratio. What’s the common ratio? It’s the constant number that you keep multiplying each term by to get the next one. In this case, you’ve already figured this out: it’s – 1/2.
If you multiply this through all of the terms on both sides of the equation, you’ll get this:
![]()
Does anything look familiar? It’s basically the same list of numbers as in the first sum equation, except it’s missing the first number, 1/2. All of the others are identical!
Subtract this second equation from the first:
![]()
The right-hand side of the equation is always going to be just the first term of the original sum. The rest of the terms on the right-hand side of the two equations are identical, so when you subtract, they become zero and disappear.
Solve for s:

This value falls between 1/4 and 1/2, so the answer is (D).
Back of the Envelope Method
There is another way to tackle this one. At the same time, this problem is really tricky—so this solution is still not an “easy” solution. Your best choice might be just to guess and move on.
Before you start reading the text, take a First Glance at the whole thing. It’s a problem-solving problem. The answers are… weird. They’re not exact. What does that mean?
Read the problem, but keep that answer weirdness in mind. The first sentence has a crazy sequence. The question asks you to sum up the first 10 terms of this sequence. And the answers aren’t exact… so apparently you don’t need to find the exact sum.
Take a closer look at the form of the answers. Notice anything about them?
They don’t overlap! They cover adjacent ranges. If you can figure out that, for example, the sum is about 3/4, then you know the answer must be (C). In other words, you can actually estimate here—you don’t have to do an exact calculation.
That completely changes the way you can approach this problem! Here’s the sequence:
![]()
According to the problem, the 10 terms are from k = 1 to k = 10. Calculating all 10 of those and then adding them up is way too much work (another clue that there’s got to be a better way to do this one). So what is that better way?
Since you know you can estimate, try to find a pattern. Calculate the first two terms (we had to do this in the first solution, too).

What’s going on? The first answer is positive and the second one is negative. Why? Ah, because the first part of the calculation is -1 raised to a power. That will just keep switching back and forth between 1 and -1, depending on whether the power is odd or even. It won’t change the size of the final answer, but it will change the sign.
Okay, and what about that second part? it went from 1/2 to 1/4. What will happen next time? Try just that part of the calculation. If k = 3, then just that part will become ![]() .
.
Interesting! So the denominator will keep increasing by a factor of 2: 2, 4, 8, 16 and so on.
Great, now you can write out the 10 numbers!
![]() … ugh. The denominator’s getting pretty big. That means the fraction itself is getting pretty small. Do I need to keep writing these out?
… ugh. The denominator’s getting pretty big. That means the fraction itself is getting pretty small. Do I need to keep writing these out?
What was the problem asking again?
Right, find the sum of these 10 numbers. Let’s see. The first number in the sequence is 1/2 and the second is -1/4, so the pair adds up to 1/4.

Right now, the answer would be right between D and E. Does the sum go up or down from here?
The third number will add 1/8, so it goes up:

But the fourth will subtract 1/16 (don’t forget that every other term is negative!), pulling it back down again:

Hmm. In the third step, it went up but not enough to get all the way to 1/2. Then, it went down again, but by an even smaller amount, so it didn’t get all the way back down to 1/4.
The fifth step would go up by an even smaller amount (1/32), and then it would go back down again by yet a smaller number (1/64). What can you conclude?
First, the sum is always growing a little bit, because each positive number is a bit bigger than the following negative number. The sum is never going to drop below 1/4, so cross off answer (E).
You keep adding smaller and smaller amounts, though, so if the first jump of 1/8 wasn’t enough to get you up to 1/2, then none of the later, smaller jumps will get you there either, especially because you also keep subtracting small amounts. You’re never going to cross over to 1/2, so the sum has to be between 1/4 and 1/2.
The correct answer is (D).
As I mentioned above, you may decide that you don’t want to do this problem at all. These aren’t that common—many people won’t see one like this on the test. Also, you don’t have to get everything right to get a top score. Just last week, I spoke with a student who outright guessed on 4 quant problems, and she still scored a 51 (the top score).
Key Takeaways for Advanced Sequence Problems
(1) Do you even want to learn how to do these? Don’t listen to your pride. Listen to your practical side. This might not be the best use of your time.
(2) All of these math problems do have a textbook solution method—but you’d have to learn a lot of math that you might never use if you try to learn all of the textbook methods. That’s not a problem if you’re great at math and have a great memory for this stuff. If not…
(3) … then think about alternate methods that can work just as well. Certain clues will indicate when you can estimate on a problem, rather than solving for the “real” number. You may already be familiar with some of these, for instance when you see the word “approximately” in the problem or answer choices that are spread pretty far apart. Now, you’ve got a new clue to add to your list: answers that offer a range of numbers and the different answer ranges don’t overlap.
* GMATPrep® questions courtesy of the Graduate Management Admissions Council. Usage of this question does not imply endorsement by GMAC.
New Year’s Resolution: Get Your GMAT Score! (Part 2)

Did you know that you can attend the first session of any of our online or in-person GMAT courses absolutely free? We’re not kidding! Check out our upcoming courses here.
How do you study? More importantly, how do you know that the way in which you’re studying is effective—that is, that you’re learning what you need to learn to improve your GMAT score? Read on! Read more
New Year’s Resolution: Get Your GMAT Score! (Part 1)

Did you know that you can attend the first session of any of our online or in-person GMAT courses absolutely free? We’re not kidding! Check out our upcoming courses here.
Whether you’ve been studying for a while or are just getting started, let’s use the New Year as an opportunity to establish or renew your commitment to getting your desired GMAT score. Read more
The 4 Math Strategies Everyone Must Master, part 2
 Last time, we talked about the first 2 of 4 quant strategies that everyone must master: Test Cases and Choose Smart Numbers.
Last time, we talked about the first 2 of 4 quant strategies that everyone must master: Test Cases and Choose Smart Numbers.
Today, we’re going to cover the 3rd and 4th strategies. First up, we have Work Backwards. Let’s try a problem first: open up your Official Guide, 13th edition (OG13), and try problem solving #15 on page 192. (Give yourself about 2 minutes.)
I found this one by popping open my copy of OG13 and looking for a certain characteristic that meant I knew I could use the Work Backwards technique. Can you figure out how I knew, with just a quick glance, that this problem qualified for the Work Backwards strategy? (I’ll tell you at the end of the solution.)
For copyright reasons, I can’t reproduce the entire problem, but here’s a summary: John spends 1/2 his money on fruits and vegetables, 1/3 on meat, and 1/10 on treats from the bakery. He also spends $6 on candy. By the time he’s done, he’s spent all his money. The problem asks how much money he started out with in the first place.
Here are the answer choices:
“(A) $60
“(B) $80
“(C) $90
“(D) $120
“(E) $180”
Work Backwards literally means to start with the answers and do all of the math in the reverse order described in the problem. You’re essentially plugging the answers into the problem to see which one works. This strategy is very closely tied to the first two we discussed last time—except, in this instance, you’re not picking your own numbers. Instead, you’re using the numbers given in the answers.
In general, when using this technique, start with answer (B) or (D), your choice. If one looks like an easier number, start there. If (C) looks a lot easier than (B) or (D), start with (C) instead.
This time, the numbers are all equally “hard,” so start with answer (B). Here’s what you’re going to do:
(B) $80
|
|
F + V (1/2) |
M (1/3) |
B (1/10) |
C $6 |
Add? |
| (B) $80 |
$40 |
…? |
$6 |
Set up a table to calculate each piece. If John starts with $80, then he spends $40 on fruits and vegetables. He spends… wait a second! $80 doesn’t go into 1/3 in a way that would give a dollar-and-cents amount. It would be $26.66666 repeating forever. This can’t be the right answer!
Interesting. Cross off answer (B), and glance at the other answers. They’re all divisible by 3, so we can’t cross off any others for this same reason.
Try answer (D) next.
|
|
F + V (1/2) |
M (1/3) |
B (1/10) |
C $6 |
Add to? |
| (B) $80 |
$40 |
…? |
$6 |
? |
|
| (D) $120 |
$60 |
$40 |
$12 |
$6 |
$118 |
In order for (D) to be the correct answer, the individual calculations would have to add back up to $120, but they don’t. They add up to $118.
Okay, so (D) isn’t the correct answer either. Now what? Think about what you know so far. Answer (D) didn’t work, but the calculations also fell short—$118 wasn’t large enough to reach the starting point. As a result, try a smaller starting point next.
|
|
F + V (1/2) |
M (1/3) |
B (1/10) |
C $6 |
Add? |
| (B) $80 |
$40 |
…? |
$6 |
? |
|
| (D) $120 |
$60 |
$40 |
$12 |
$6 |
$118 |
| (C) $90 |
$45 |
$30 |
$9 |
$6 |
$90 |
It’s a match! The correct answer is (C).
Now, why would you want to do the problem this way, instead of the “straightforward,” normal math way? The textbook math solution on this one involves finding common denominators for three fractions—somewhat annoying but not horribly so. If you dislike manipulating fractions, or know that you’re more likely to make mistakes with that kind of math, then you may prefer to work backwards.
Note, though, that the above problem is a lower-numbered problem. On harder problems, this Work Backwards technique can become far easier than the textbook math. Try PS #203 in OG13. I would far rather Work Backwards on this problem than do the textbook math!
So, have you figured out how to tell, at a glance, that a problem might qualify for this strategy?
It has to do with the form of the answer choices. First, they need to be numeric. Second, the numbers should be what we consider “easy” numbers. These could be integers similar to the ones we saw in the above two problems. They could also be smaller “easy” fractions, such as 1/2, 1/3, 3/2, and so on.
Further, the question should ask about a single variable or unknown. If it asks for x, or for the amount of money that John had to start, then Work Backwards may be a great solution technique. If, on the other hand, the problem asks for x – y, or some other combination of unknowns, then the technique may not work as well.
(Drumroll, please) We’re now up to our fourth, and final, Quant Strategy that Everyone Must Master. Any guesses as to what it is? Try this GMATPrep© problem.

“In the figure above, the radius of the circle with center O is 1 and BC = 1. What is the area of triangular region ABC?
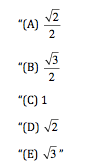
If the radius is 1, then the bottom line (the hypotenuse) of the triangle is 2. If you drop a line from point B to that bottom line, or base, you’ll have a height and can calculate the area of the triangle, since A = (1/2)bh.
You don’t know what that height is, yet, but you do know that it’s smaller than the length of BC. If BC were the height of the triangle, then the area would be A = (1/2)(2)(1) = 1. Because the height is smaller than BC, the area has to be smaller than 1. Eliminate answers (C), (D), and (E).
Now, decide whether you want to go through the effort of figuring out that height, so that you can calculate the precise area, or whether you’re fine with guessing between 2 answer choices. (Remember, unless you’re going for a top score on quant, you only have to answer about 60% of the questions correctly, so a 50/50 guess with about 30 seconds’ worth of work may be your best strategic move at this point on the test!)
The technique we just used to narrow down the answers is one I’m sure you’ve used before: Estimation. Everybody already knows to estimate when the problem asks you for an approximate answer. When else can (and should) you estimate?
Glance at the answers. Notice anything? They can be divided into 3 “categories” of numbers: less than 1, 1, and greater than 1.
Whenever you have a division like this (greater or less than 1, positive or negative, really big vs. really small), then you can estimate to get rid of some answers. In many cases, you can get rid of 3 and sometimes even all 4 wrong answers. Given the annoyingly complicated math that sometimes needs to take place in order to get to the final answer, your best decision just might be to narrow down to 2 answers quickly and then guess.
Want to know how to get to the actual answer for this problem, which is (B)? Take a look at the full solution here.
The 4 Quant Strategies Everyone Must Master
Here’s a summary of our four strategies.
(1) Test Cases.
– Especially useful on Data Sufficiency with variables / unknowns. Pick numbers that fit the constraints given and test the statement. That will give you a particular answer, either a value (on Value DS) or a yes or no (on Yes/No DS). Then test another case, choosing numbers that differ from the first set in a mathematically appropriate way (e.g., positive vs. negative, odd vs. even, integer vs. fraction). If you get an “always” answer (you keep getting the same value or you get always yes or always no), then the statement is sufficient. If you find a different answer (a different value, or a yes plus a no), then that statement is not sufficient.
– Also useful on “theory” Problem Solving questions, particularly ones that ask what must be true or could be true. Test the answers using your own real numbers and cross off any answers that don’t work with the given constraints. Keep testing, using different sets of numbers, till you have only one answer left (or you think you’ve spent too much time).
(2) Choose Smart Numbers.
– Used on Problem Solving questions that don’t require you to find something that must or could be true. In this case, you need to select just one set of numbers to work through the math in the problem, then pick the one answer that works.
– Look for variable expressions (no equals or inequalities signs) in the answer choices. Will also work with fraction or percent answers.
(3) Work Backwards.
– Used on Problem Solving questions with numerical answers. Most useful when the answers are “easy”—small integers, easy fractions, and so on—and the problem asks for a single variable. Instead of selecting your own numbers to try in the problem, use the given answer choices.
– Start with answer (B) or (D). If a choice doesn’t work, cross it off but examine the math to see whether you should try a larger or smaller choice next.
(4) Estimate.
– You’re likely already doing this whenever the problem actually asks you to find an approximate answer, but look for more opportunities to save yourself time and mental energy. When the answers are numerical and either very far apart or split across a “divide” (e.g., greater or less than 0, greater or less than 1), you can often estimate to get rid of 2 or 3 answers, sometimes even all 4 wrong answers.
The biggest takeaway here is very simple: these strategies are just as valid as any textbook math strategies you know, and they also require just as much practice as those textbook strategies. Make these techniques a part of your practice: master how and when to use them, and you will be well on your way to mastering the Quant portion of the GMAT!
Read The 4 Math Strategies Everyone Must Master, Part 1.
The 4 Math Strategies Everyone Must Master, Part 1
We need to know a lot of different facts, rules, formulas, and techniques for the Quant portion of the test, but there are 4 math strategies that can be used over and over again, across any type of math—algebra, geometry, word problems, and so on.
Do you know what they are?
Try this GMATPrep® problem and then we’ll talk about the first of the 4 math strategies.
*If mv < pv < 0, is v > 0?
(1) m < p
(2) m < 0
All set? Read more
Tackling Multi-Shape Geometry on the GMAT
What do you do when you realize a geometry problem has just popped up on the screen? Try this GMATPrep© problem from the free practice test and then we’ll talk about what to do!

In the figure above, the radius of the circle with center O is 1 and BC = 1. What is the area of triangular region ABC?
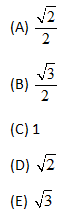
What’s your first step? Let’s use this problem as an opportunity to practice the Quant Process.

At a glance, you can see that the problem provides a diagram. Draw! Make it big enough that you can add labels as you calculate new pieces of information (and, of course, jot down any information given in the problem).
Finally, write down any formulas you’ll need, as well as whatever the problem asks you to find. Your scrap paper might look something like this:
Read more
News from the GMAC Summit (from the makers of the GMAT)
 Last Friday, I attended the biannual GMAC Summit, a special conference that the makers of the GMAT put on for test prep companies. I want to share various tidbits that you should know!
Last Friday, I attended the biannual GMAC Summit, a special conference that the makers of the GMAT put on for test prep companies. I want to share various tidbits that you should know!
Integrated Reasoning (IR) has existed long enough now that GMAC is starting to be able to draw some conclusions about the efficacy of the section. Dr. Lawrence Rudner, chief psychometrician of GMAC, is quite pleased with the section’s performance to date.
Though they still need to collect more data to be sure, early results indicate that IR is actually a little bit better of a predictor of grades in business school than are the quant and verbal scores. It will still be a while before they can collect as solid / extensive data as they have for quant and verbal, but perhaps it will be the case that, eventually, IR will become the most important section! (Don’t worry: if you are applying right now, nothing has changed. Even if you aren’t planning to apply until next year, it’s unlikely that the importance of IR will change extensively by then.)
There were no admissions officers in attendance, but we did hear from GMAC that they have heard that admissions consultants are starting to consider using IR as a tiebreak for borderline cases. For example, let’s say a school considers 680+ a strong score and 630 to 670 an average score. For the pool of 630 to 670 candidates (only a few of whom are likely to be admitted), one potential tiebreak is the IR score.
If IR is not your thing, don’t worry: it’s unlikely that any school is making this tiebreak decision based solely on the IR score. After all, many different variables go into an application; they might also decide to use number of years of work experience, under-represented industries, or some other factor. If you do tend to perform well on IR, though, then bonus: that’s an extra mark in the plus column for you.
Interestingly, US students are tending to do a bit better on IR than all other students. (This is also true for the Verbal section of the test, while non-US students tend to do better than US students on the quant section of the test.) A lot of people consider IR more of a quant section, but verbal is just as important. If quant is your strength, then you’ll feel that IR is testing verbal more, and vice versa.
Scoring and Timing
I have only one piece of info for you here, but it’s quite an important piece of data. As we were discussing the scoring algorithm, someone asked the age-old question: whether certain questions were “worth more” than others. Dr. Rudner indicated (as he always has in the past) that the earlier questions are not worth more than the later ones. He did, though, indicate something that we suspected but had never heard officially confirmed: “outlier” questions ultimately count less towards your score.
What’s an outlier? Briefly, an outlier is a question for which your performance was unexpected. Read on to understand what this means.
An outlier is always relative to your own performance. (Note: we’re also talking only about the questions that count towards your score; the experimentals don’t matter here.) Most of the questions you answer will be within a certain range of difficulty. As a general rule, you’ll answer more of the easier questions in your range correctly and you’ll answer more of the harder questions incorrectly. This is the expected behavior.
Read more
What Kind Of CR Question Is This? (part 3)
 We’ve been on a CR kick lately! In the first two parts of this series, we talked about how to tackle Fill in the Blank and Complete the Passage questions. This time, I’ve got something different for you: a question that looks very familiar at first glance but turns a bit… well, weird.
We’ve been on a CR kick lately! In the first two parts of this series, we talked about how to tackle Fill in the Blank and Complete the Passage questions. This time, I’ve got something different for you: a question that looks very familiar at first glance but turns a bit… well, weird.
Let’s try it before I say anything more. This GMATPrep© problem is from the two free exams that come with the GMATPrep software. Give yourself about 2 minutes (though it’s okay to stretch to 2.5 minutes on a CR as long as you are making progress.)
“On of the limiting factors in human physical performance is the amount of oxygen that is absorbed by muscles from the bloodstream. Accordingly, entrepreneurs have begun selling at gymnasiums and health clubs bottles of drinking water, labeled “SuperOXY,” that has extra oxygen dissolved in the water. Such water would be useless in improving physical performance, however, since the amount of oxygen in the blood of someone who is exercising is already more than the muscle cells can absorb.
Which of the following, if true, would serve the same function in the argument as the statement in boldface?
“(A) world-class athletes turn in record performances without such water
“(B) frequent physical exercise increases the body’s ability to take in and use oxygen
“(C) the only way to get oxygen into the bloodstream so that it can be absorbed by the muscles is through the lungs
“(D) lack of oxygen is not the only factor limiting human physical performance
“(E) the water lost in exercising can be replaced with ordinary tap water”
Step 1: Identify the Question
The boldface font is immediately obvious, of course. Boldface denotes a Describe the Role question.
The question stem does have one little idiosyncrasy, though: it asks what answer would serve the same function. Normally, Role questions ask what function the boldface statement plays in the argument. The question stem also contains “if true” wording, which we normally see on Strengthen, Weaken, or Discrepancy (paradox) questions.
Glance at the answers. Notice anything? This is not what Role answers typically look like! Usually they say something such as “The statement provides evidence supporting the author’s claim” or similar.
What’s going on here? Read the argument.
Step 2: Deconstruct the Argument
Here’s what I thought and wrote while I did the problem. Your own thought process won’t be exactly the same as mine and, of course, your notes will probably look quite different, since we all have our own ways of abbreviating things. (Note: R = role; note that I put a question mark next to it because I wasn’t 100% sure what was actually going on).

So back to that weird question stem. If this were just a straight Role question, then what would the answer be? The boldface statement is support for the conclusion; it’s a premise.
But what’s the goal for this question?
Step 3: State the Goal
The answers don’t describe the existing boldface statement. Rather, they contain new facts that we’re supposed to accept as true. Further, the question asked us to find an answer that “would serve the same function” as the original statement.
What function did the original statement serve? Aha! The original statement served as a premise to support the conclusion. So we need to find another statement that serves that same purpose.
Will it support the conclusion in exactly the same way? I’m really not sure. (Seriously! When I first saw this question, I didn’t know!) So I’m going to keep an open mind and look for anything that could support the conclusion in general.
Work from Wrong to Right

The correct answer is (C).
Interesting. We just learned something new. Most Describe the Role (or Boldface) questions ask us to describe the role of the given statement. We might be asked, though, to demonstrate our knowledge of the role by finding a different, completely new statement that serves the same role as the original statement in the argument.
What do we have to do? We have to “decode” the original statement (in the above case, we had a premise supporting the conclusion) and then we have to find another statement that could also serve as a premise.
That new premise might be really different from the original premise. In this problem, the original premise focused on the oxygen already in our blood. The new premise, answer (C), provided a different piece of the puzzle: we have to take oxygen in through our lungs in order to get that oxygen into the bloodstream. Either piece of information serves to support the idea that OXY is useless, but each does so in different ways.
Take-aways for “Same Function As” Role Questions:
(1) The standard task on role questions is to describe the role of the statement given in the argument.
(2) You might see a variation on this standard task: you may be asked to find a new statement that plays the same role as the original.
(3) This new statement may discuss a different aspect of the argument. That’s perfectly all right as long as the statement overall plays the same role as the original boldface statement.
* GMATPrep® questions courtesy of the Graduate Management Admissions Council. Usage of this question does not imply endorsement by GMAC.
What Kind Of Critical Reasoning Question Is This? Part 1
I was talking to a student today about Complete the Passage CR arguments (people also call these the Fill in the Blank questions). The student was struggling with these and talking about them as though they were their own category. The problem: they’re not actually a separate category at all!
Try this GMATPrep © problem out (it’s from the free set that comes with the software) and then we’ll talk about it. Give yourself about 2 minutes (though it’s okay to stretch to 2.5 minutes on a CR as long as you are making progress.)
“Which of the following best completes the passage below?
“People buy prestige when they buy a premium product. They want to be associated with something special. Mass-marketing techniques and price reduction strategies should not be used because ________________
“(A) affluent purchasers currently represent a shrinking portion of the population of all purchasers
“(B) continued sales depend directly on the maintenance of an aura of exclusivity
“(C) purchasers of premium products are concerned with the quality as well as with the price of the products
“(D) expansion of the market niche to include a broader spectrum of consumers will increase profits
“(E) manufacturing a premium brand is not necessarily more costly than manufacturing a standard brand of the same productâ€
Step 1: Identify the Question
The blank line immediately leaps to eye of course: as soon as you see that, you know you have an argument in the “complete the passage†format.
What kind of question type is it? Actually these fall into one of the regular types that you already know: Strengthen, Weaken, Find the Assumption, Inference, and so on. The trick is that it’s a bit harder to tell which type.
The majority of Complete the Passage questions are Strengthen. The second most common category is Find the Assumption. Typically, if you see the word because or since right before the underline (as in this problem), then you probably have a Strengthen question. The word because (or since) indicates that the correct answer will add a piece of evidence to support some statement. You’ll need to read the argument to be sure, but you can have a pretty strong hunch.
Step 2: Deconstruct the Argument
This is likely a strengthen question, so it should contain a conclusion.
Here’s what I thought and wrote while I did the problem. Your own thought process won’t be exactly the same as mine and, of course, your notes will probably look quite different, since we all have our own ways of abbreviating things. (Note: S = strengthen; at first I put a question mark next to it because I wasn’t 100% sure until I finished the argument.)
If the conclusion is NOT to use mass-marketing techniques and price reduction strategies because of some reason, then that reason must support that conclusion. This is, indeed, a Strengthen question.
Step 3: State the Goal
The goal on Strengthen questions is to find a new piece of information that makes the conclusion at least a little more likely to be valid. I’m trying to validate the idea that you should NOT use certain strategies. (Note: in Complete the Passage format, sometimes the correct answer won’t really be new; it will mostly just restate something that the argument already said. This is acceptable as long as it strengthens!)
Why not? The first two sentences said that premium products are all about prestige and “something special.†If you’re trying to sell premium products, then, mass-market techniques probably aren’t going to make people feel “special.†Likewise, a reduction in price doesn’t scream “premium product!†We expect premium products to cost more and we don’t expect everyone in the world to have them.
I’m going to keep that in mind while I examine the answers!
Work from Wrong to Right
The correct answer is (B).
Note that answers (A) and (D) both seem to go along with the idea that we might want to use mass-marketing techniques or price-reduction strategies. Both are trap answers designed to catch someone who didn’t notice or forgot that the conclusion says these strategies should NOT be used.
Looking for more help on Critical Reasoning? Check out the Master Resource List for Critical Reasoning.
Take-aways for Complete the Passage formats:
(1) These are not a separate question type. A “complete the passage†question falls into one of the same categories as all other questions; you have to figure out which it is.
(2) Most often, these questions are Strengthen (as in the above case) or Find the Assumption. If you see the word because or since right before the underline, you probably have a Strengthen question. If you see something else, then you may have an Assumption question instead.
(3) As with any CR question, the key is to identify the type of question and follow the standard process from there!
* GMATPrep © questions courtesy of the Graduate Management Admissions Council. Usage of this question does not imply endorsement by GMAC.”